Реферат: Оценка надежности

(14)

Область интегрирования находится из условия l(t)= l(x₁ , x₂ , x₃ …x_m ;t)< l*. Вероятность отказа по критерию остаточного ресурса находится как вероятность выполнения неравенства l(t)>l*: . При известных законах распределения p1(l,t) и pl*(l*), определяемым по формулам (12) и (14), эта вероятность находится как

(15)

Формулу (15) можно упростить проинтегрировав по одной из переменных в области D[l,t,l*]:

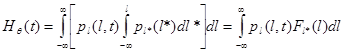(16)

Другую эквивалентную форму получим, взяв в качестве независимой переменной l*:

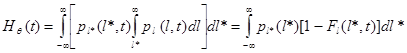(17)

Рассмотренная схема оценки вероятности отказов по критерию остаточного ресурса учитывает рост одиночного дефекта. При наличии множества начальных дефектов с различными размерами будем считать, что их рост происходит независимо. Разобьем весь интервал начальных размеров дефектов, как обнаруженных в результате контроля, так и пропущенных, на подинтервалы со средними начальными размерами l_k . Обозначим через _k математическое ожидание числа дефектов, попавших в k-ый интервал. Эта величина находится через математическое ожидание k_k числа обнаруженных в результате контроля дефектов в k-ом интервале и через вероятность их обнаружения Р_а (l_k )по формуле: .

Суммарная вероятность отказов при наличии множества дефектов находится как:

(18)

здесь через H_k (t) обозначена вероятность отказов, вычисленная по формуле (16) или (17) при начальном размере дефекта l_k .

Окончательно с учетом вероятности отказов к моменту контроля t₀ для вероятности отказов в момент времени t>t₀ получим:

H(t)=H₀ +H_ (t) (19)

где вероятность H₀ находится по формуле (8).

По формуле (19) можно оценит увеличение риска с течением времени эксплуатации после очередного контроля. Эта формула позволяет также оценить остаточный ресурс из условия непревышения вероятностью отказов предельного значения H*. Расчетное значение остаточного ресурса * находится как корень уравнения H()=H*.

Учет различных типов дефектов производится по формуле:

(20)

где вероятности отказов H_j (t) для каждого типа дефектов находятся согласно (19).

Для численного примера аппроксимируем функцию распределения длин дефектов F(l) и критических дефектов асимптотическими распределениями Вейбулла с параметрами l₀ , l*₀ , l_c , l*_c , a, a₁ :

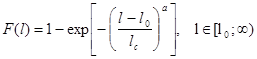(21)

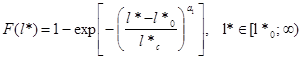(22)

Математическое ожидание числаобнаруженных дефектов аппроксимируем зависимостью с параметрам ₁ и l₁ : .

Уравнение роста дефектов (10) перепишем в виде:

(23)

При =const решение этого уравнения с начальным условием l_k (t₀ )= l_0k имеет вид: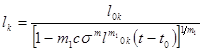 , где m₁ =m/2-1 (24)

Рассматриваяпараметр напряжения  как случайный с распределением Релея

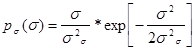(25)

Найдем распределение длин дефектов F_l (l_k ;t) по формуле (12), которая примет вид:

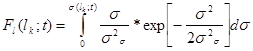(26)