Реферат: Оценка систем дистанционного образования (математическая модель)

Фундаментальная матрица после вычислений примет вид:

Тогда, согласно формуле (5), матрица вероятностей поглощения вычисляется так:

.

Поясним вероятностный смысл полученной матрицы с помощью конкретных чисел. Пусть, а. Тогда после подстановки полученных значений в матрицу получим:

Таким образом, если процесс начался в , то вероятность попадания его в равна , а в - . Отметим одно интересное обстоятельство: несмотря на то, что, казалось бы, левое поглощающее состояние (“левая яма”) находится рядом с , но вероятность попадания в нее почти в два раза меньше, чем в “удаленную яму” - . Этот интересный факт подмечен в теории ДМЦ, и объясняется он тем, что , то есть процесс имеет как бы “правый уклон”. Рассмотренная выше модель называется в теории ДМЦ моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр.

В частности, в рассмотренном примере объясняется тот факт, что более сильный игрок может дать заранее значительное преимущество (“фору”) слабому противнику и все равно его шансы на выигрыш будут более предпочтительными.

Кроме указанных выше средних характеристик вероятностного процесса с помощью фундаментальной матрицы можно вычислить моменты и более высоких порядков. В частности, дисперсия числа пребывания в том или ином состоянии - D определяется с помощью следующей матрицы:

(6)

где

- диагональная матрица, т.е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (3а) будет иметь вид:

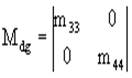
В свою очередь, матрица М представляет собой матрицу, полученную из М путем возведения в квадрат каждого ее элемента, то есть для (3а) будем иметь:

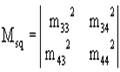
Аналогичным образом определяема и дисперсия для общего количества раз пребывания в том или ином состоянии . Обозначим ее :

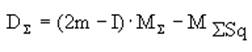
3.2. Марковские цепи в прогнозирование учебного процесса

Проанализируем вероятность окончания ВУЗа студентом при традиционной форме обучения. Процесс получения образования опишем в терминах поглощающих Марковских цепей[2] .

Пусть s1, …, s5 – состояния «Первокурсник», …, «Пятикурсник», s6 – «Отчислен», s7 – «Получил диплом». Вероятность завершения каждого курса: pi,i+1 (i Î 1 ¸ 4) = 0.91[3] , а вероятность отчисления pi (i Î 1 ¸ 5) = 0.09. Тогда матрица переходных вероятностей {pij} в канонической форме будет иметь вид:

S7	S6	S1	S2	S3	S4	S5
S7	1	0	0	0	0	0	0
S6	0	1	0	0	0	0	0
S1	0	0.09	0	0.91	0	0	0
S2	0	0.09	0	0	0.91	0	0
S3	0	0.09	0	0	0	0.91	0
S4	0	0.09	0	0	0	0	0.91
S5	0.91	0.09	0	0	0	0	0

(табл. 1).

При начальных условиях p0,1 = 1 вероятность успешного окончания ВУЗа p5-7 = 0.61, т.к. из 100 поступивших через 5 лет дипломы получат лишь 61 человек.

Рассмотрим ситуацию при дистанционной форме обучения. Обозначения оставим прежними. Матрица переходных вероятностей {pij} в этом случае имеет другой вид:

S7	S6	S1	S2	S3	S4	S5
S7	1	0	0	0	0	0	0
S6	0	1	0	0	0	0	0
S1	0	0.01	0.1	0.8	0.05	0.03	0.01
S2	0.01	0.01	0	0.1	0.8	0.05	0.03
S3	0.03	0.01	0	0	0.1	0.8	0.06
S4	0.09	0.01	0	0	0	0.1	0.8
S5	0.89	0.01	0	0	0	0	0.1

(табл. 2).

Выполнив расчеты для матрицы из таб. 2, получим, что p5-7 = 0.68, а p4-7 = 0.25, т.е. уже через четыре года примерно четвертая часть студентов получат дипломы.

Матрица из табл. 2 может использоваться для анализа вариантов организации дистанционного образования и прогнозирования характеристик образовательного процесса.

Таким образом, в снижении стоимости образовательного процесса в целом можно выделить три основных тенденции:

разработку и внедрение информационных систем управления учебным процессом;