Реферат: Оцінювання параметрів розподілів

Звичайно використовують рівень надійності, що має значення: 0,95; 0,99 і 0,999.

Довірчим називають інтервал ( ), який покриває невідомий параметр із заданою надійністю .

1 Довірчі інтервали для оцінки математичного сподівання нормаль­ного розподілу при відомому . Розглянемо задачу інтервальної оцінки невідомого математичного сподівання кількісної ознаки по вибірковій
середній нормально розподіленої сукупності з відомим середньо квадратич­ним відхиленням . Знайдемо довірчий інтервал, що покриває параметр з надійністю .

Вибіркова середня змінюється від вибірки до вибірки. Тому її можна розглядати, як випадкову величину , а вибіркові значення ознаки , , ... , (ці числа також змінюються від вибірки до вибірки) – як однаково розподілені незалежні випадкові величини , , ... , . Тобто, математичне сподівання кожної з цих величин дорівнює і середнє квадратичне відхилення – .

Можна показати, що у разі нормального розподілення випадкової величина вибіркова середня , знайдена за незалежними спостереженнями, також розподілена нормально з параметрами:

, . (12)

Поставимо вимогу, щоб було виконано співвідношення

, (13)

де – задана надійність.

Застосуємо до нормально розподіленої випадкової величини відому з теорії ймовірностей формулу про ймовірність відхилення нормально розподіленої випадкової величини зі середньоквадратичним відхиленням від його математичного сподівання не більше ніж на

, (14)

де – табульована функція Лапласа (3).

При цьому у формулі (14) відповідно до (12) необхідно замінити на , на , залишивши математичне чекання без зміни.

Тоді одержимо:

, (15)

де введено таке позначення

. (16)

Підставивши у формулу (15) вираз величини через з (16)

, (17)

перетворивши її до вигляду:

.

З огляду на те, що ймовірність задана і дорівнює (13), а також, що випадкова величина є формальним поданням вибіркової середньої , остаточно одержимо:

. (18)

Цю оцінку називають класичною. Відповідно до неї з надійністю можна стверджувати, що довірчий інтервал покриває невідомий параметр . При цьому величина визначається з рівності (18), а точність оцінки – з (17).

З формули (17) видно, що із зростанням обсягу вибірки величина зменшується, тобто точність оцінки підвищується. З співвідношення (18), де , із врахуванням відомого зростаючого характеру функції Лапласа (3), випливає, що підвищення надійності класичної оцінки (18) призводить до погіршення її точності.

2 Довірчі інтервали для оцінки математичного сподівання нормального розподілу при невідомому . Ускладнимо постановку задачі, розглянутої в попередньому пункті, вважаючи, що тепер середнє квадратичне відхилення нормально розподіленої кількісної ознаки невідомо.

У цьому випадку за даними вибірки побудуємо випадкову величину (її значення будемо традиційно позначати відповідною малою буквою ), що є функціональним перетворенням випадкової величини , введеної в попередньому пункті:

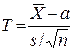. (19)

Тут збережено позначення, які введені в попередньому пункті. Крім того, вжито , що є "виправлене" середнє квадратичне відхилення (1.7).