Реферат: Оцінювання параметрів розподілів

,

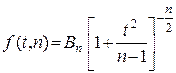Де

,

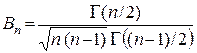– Гама-функція Эйлера (2.4).

Очевидно, що розподіл Стьюдента визначається параметром – обсягом вибірки та не залежить від невідомих параметрів і , що зумовило його практичну цінність. Оскільки функція є парною відносно , ймовірність виконання нерівності 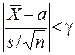можна перетворити таким чином:

.

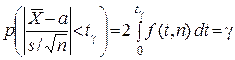При заміні нерівності в круглих дужках на еквівалентну йому подвійну нерівність і заміні на так само, як у попередньому пункті, остаточно одержимо:

.

Тобто, використовуючи розподіл Стьюдента, можна знайти довірчий інтервал , що покриває невідомий параметр із надійністю . Величина при цьому знаходиться в таблиці розподілу Стьюдента у залежності від значень параметрів і .

3 Довірчі інтервали для оцінки середнього квадратичного відхилення нормального розподілу. Тепер вирішимо задачу інтервальної оцінки з надійністю невідомого генерального середнього квадратичного відхилення нормально розподіленої кількісної ознаки за його "виправленим" вибірковим середньо квадратичним відхиленням s. Це означає, що має виконуватися умова:

чи, що те ж саме,

. (20)

Подвійну нерівність у виразі (20) зручно перетворити до вигляду:

(21)

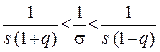, (22)

де введено позначення

(23)

і враховано, що відхилення відносно , тобто – мала величина в порівнянні з , так що .

Вибіркове середнє квадратичне відхилення змінюється від вибірки до вибірки, тому його можна розглядати як випадкову величину, що ми дотримуючись традиції позначимо відповідною великою літерою . Помноживши всі члени останньої нерівності (22) на , одержимо нову нерівність

,

що після введення позначення

(24)

прийме остаточний вигляд:

. (25)

Відзначимо, що нерівності (21) і (25) еквівалентні. Тому рівність (20) можна тепер переписати так:

. (26)

Пірсон показав, що величина (24) після її підвищення до квадрату, тобто у вигляді , підкоряється закону розподілу "хі-квадрат" (5), тому і має таке позначення. Можна показати, що щільність розподілу самої випадкової величини має при цьому наступний вигляд: