Реферат: Ответы по геометрии для 9 класса
61. Формулы для радиусов вписанных и описанных окружностей правильного n-угольника (формулы и примеры).
62. Свойство диагоналей ромба.
63. Задача по теме «Равнобедренный треугольник».
64. Задача по теме «Подобие треугольников».
65. Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника (формулы и примеры).
66. Свойство диагоналей прямоугольника.
67. Задача по теме «Равнобедренный треугольник».
68. Задача по теме «Параллельные прямые».
69. Первый признак равенства треугольников.
70. Задача по теме «Площадь».
71. Задача по теме «Многоугольники».
72. Формулы площади треугольника (формулы и примеры).
73. Признак параллелограмма.
74. Задача по теме «Равнобедренный треугольник».
75. Задача по теме «Углы, вписанные в окружность».
76. Формулы площади прямоугольника и параллелограмма (формулы и примеры).
77. Второй признак равенства треугольников.
78. Задача по теме «Средняя линия треугольника».
79. Формула площади трапеции (формула и пример).
80. Признак равенства прямоугольных треугольников.
81. Задача по теме «Векторы».
82. Задача по теме «Окружность, вписанная в треугольник».
83. Формула площади круга (формула и пример).
84. Теорема Пифагора.
85. Задача по теме «Окружность, описанная около треугольника».
86. Задача по теме «Геометрическое место точек».
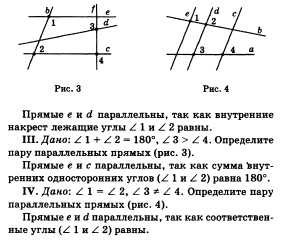
1. Признаки параллельности прямых (формулировки и примеры).
I. Две прямые, параллельные третьей* параллельны.
II. Если внутренние накрест лежащие углы равны, то прямые параллельны
III. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.
IV. Если соответственные углы равны, то прямые параллельны.

2. Решение треугольника по стороне и двум углам.
Решить треугольник по стороне и двум прилежащим к ней углам — это значит при заданных стороне и двум прилежащим к ней углам найти третий угол и две другие стороны.
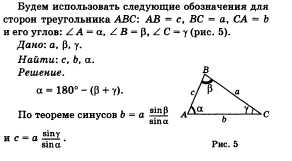
Единственность решения вытекает из признака равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. Задача по теме «Углы, вписанные в окружность».
