Реферат: Перемещение и напряжение при ударе. Испытание материалов ударной нагрузкой

После преобразований получим следующее квадратное уравнение для определения силы удара :

(14)

где — радиус инерции сечения относительно оси х ;

— статическое укорочение стержня;

— гибкость стержня относительно оси х.

Определив из этого уравнения, можно по формуле (4) определить перемещение в точке удара. Напряжения при сжимающем ударе найдутся из формулы

(15)

Если деформации стержня малы по сравнению с высотой падения h , то, приравнивая работу силы Q, равную А = Qh , потенциальной энергии деформации (11.13), получим

(16)

Откуда

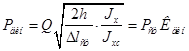(17)

где —динамический коэффициент, равный

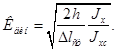(17а)

Напряжения равны

(18)

Аналогичным способом можно получить решение задачи и в общем случае удара, когда точка удара не лежит ни на одной из главных осей поперечного сечения стержня.

Пример 2. Определить силу удара и напряжения от падающего груза весом Q в стержне круглого сечения для двух случаев: 1) центрального удара; 2) внецентренного удара при а = r .

Решение. Динамические коэффициенты вычисляем по приближенным формулам, считая, что h велико по сравнению с .

1. Центральный удар.

Динамический коэффициент вычисляем по формуле (2а)

2. Внецентренный удар . определяем по формуле (17а)

Сравнивая результаты, видим, что при центральном ударе сила удара Р_днн в 2,24 раза больше, чем при внецентренном ударе, а напряжения в 0,43 раза меньше.

Из этого следует, например, что при забивке свай выгодно центрировать удар для того, чтобы увеличивать силу удара, погружающую сваю в грунт и уменьшать динамические напряжения за счет ликвидации изгибающего момента, не оказывающего влияния на погружение сваи.

Для центрирования удара наголовник для сваи следует делать с центрирующим выступом (рис. 11.4, б).