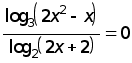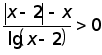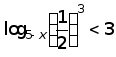Реферат: Показникові та логарифмічні рівняння, нерівності та їх системи в шкільному курсі математики
![]()
![]()
Поглиблений рівень
Розв’язати рівняння.
Розв’язати нерівності
![]()
| Логіко- дидактичний аналіз при вивченні теми | ||
| " Показникова функція" | ||
| Зона І | Зона ІІ | |
| Статус | Навчальний матеріал, який | Навчальний матеріал, який |
| актуально сприймається | актуально контролюється | |
| (зона найближчого розвитку) | (зона актуального розвитку) | |
| П | 1. Показникова функція. | 1.1. Узагальненне поняття степеня |
| 1.2. Властивості арифметичного | ||
| кореня | ||
| Ф | 2.Задачі на побудову графіків | 2.1. Властивості степеня з |
| раціональним показником | ||
| Т | 3. Властивості показникової | 3.1. Властивості степеня з |
| функції | дійсним показником | |
| Т | 4. Властивості графіка | |
| показникової функції | ||
| Ф | 5. Застосування властивостей | 5.1. Властивості степеня з |
| показникової функції в | дійсним показником | |
| математиці | 5.2. Спадна і зростаюча функції | |
| Ф | 6. Застосування властивостей | 6.1. Властивості степеня з |
| показникової функції в | дійсним показником | |
| практиці | 6.2. Радіоактивний розпад | |
| 6.3. Атмосферний тиск | ||
| Ф | 7. Основні показникові | 7.1.Узагальнене поняття степеня |
| тотожності | ||
| П | 8. Показникові рівняння | |
| Ф | 8'. Найпростіші | 8'.1.Узагальнене поняття степеня |
| показникові рівняння. | ||
| Ф | 8''. Типи і методи | 8''.1. Властивості степеня з |
| розв'язання показникових | дійсним показником | |
| рівнянь | ||
| Ф | 8'''. Показникові нерівності | 8'''.1.Властивості степеня з |
| дійсним показником | ||
| Логіко- дидактичний аналіз при вивченні теми | ||
| " Логарифмічна функція" | ||
| Зона І | Зона ІІ | |
| Статус | Навчальний матеріал, який | Навчальний матеріал, який |
| актуально сприймається | актуально контролюється | |
| (зона найближчого розвитку) | (зона актуального розвитку) | |
| Ф | 1. Вступ | |
| П | 2. Логарифм | 2.1.Узагальнене поняття степеня |
| Ф | 3.Ілюстративні вправи | 3.1. Показникова рівність ab=N |
| Ф | 4. Задачі на логарифм | |
| П | 5. Десяткові логарифми | |
| Ф | 6. Ілюстративні задачі | |
| Т | 7. Основна логарифмічна | 7.1. Властивості степеня з |
| тотожність | дійсним показником | |
| 7.2. Показникова рівність | ||
| Ф | 8. Ілюстративні вправи | |
| Т | 9. Основні властивості | |
| логарифмів | ||
| СД | 10. Логарифмування виразів | |
| Т | 11. Тотожності, що містять | 11.1. Властивості степеня з |
| логарифми | дійсним показником | |
| Ф | 12. Ілюстративні вправи | |
| СД | 13. Потенціювання | |
| Ф | 14. Ілюстративні вправи | |
| СД | 15. Перехід від однієї основи | |
| логарифмів до іншої | ||
| Ф | 16. Ілюстративні вправи | |
| П | 17. Натуральні логарифми | |
| П | 18. Логарифмічна функція | 18.1. Узагальнене поняття степеня |
| Т | 19. Зв'язок між показниковою | 19.1. Узагальнене поняття степеня |
| і логарифмічною функціями | 19.2. Поняття оберненої функції | |
| Ф | 20. Ілюстративні вправи | |
| Т | 21. Властивості логарифмічної | 21.1. Властивості показникової |
| функції | функції | |
| Т | 22. Спільні властивості | |
| логарифмів для конкретних | ||
| випадків | ||
| Ф | 23. Ілюстративні вправи | 23.1. Область визначення функції |
| П | 24. Логарифмічні рівняння | |
| П | 25. Застосування | |
| логарифмічної функції до | ||
| розв'язування рівнянь і | ||
| нерівностей. | ||
-
Використання нових інформаційних технології при вивченні тем показникові і логарифмічні рівняння та нерівності.
Хочу поділитися своїми враженнями від нової форми навчання - за допомогою комп’ютера. Звичайно, не можна все зводити до нього, - і кількість годин, проведенних за екраном, не може служити критерієм якості навчання, як це намагаються представити в деяких приватних школах. Але безсумнівно одне - комп’ютер відмінний помічник для организації індивідуального навчання. Бо як тільки педагог перестає бачить в учені просто сосуд, який треба наповнити знаннями та вміннями, йому доводиться шукати індивідуальний підхід до кожного, підстраюватися до його інтересів, темп засвоєння матеріалу, особисті особливості психіки. Наприклад, в деяких школах кожен учень може вибрати для себя не просто курс, який його цікавить, але навіть окремі предмети. Комп’ютер, як відомо, виконує ту программу, яка в нього закладена, і надає великий вибір тем для вивчення. Сучасні методи представлення інформації в комп’ютерах включають в себе не просто текст, але і картинки, відео, звукові фрагменти. Це дозволяє задіяти практично всі органи почуттів, використовуваємих для сприйняття інформації, при цьому здійснюється її дублювання по різним каналам сприйняття, що різко підвищує швидкість і якість засвоєння матеріалу. Комп’ютерный підручник неможна вже порівнювати з книгою, як це було всього декілька років тому - зараз більшість навчаючих програм неможливо відрізнити від ігр, і для того, щоб перемогти в такій грі, будуть потрібні знання, які дитині важко приїняти як необхідні йому тільки зараз - але ж всім нам притаманно відкладати "на потім" рішення багатьох проблем. А такий елемент сучасних комп’ютерних документів, як гипертекстова ссилка дозволяє при необхідності звернутися до будь-якого місця документа за додатковою інформацією, і втой же час при повторному вивченні не перевантажує початковий текст документу. Доречі, по принципу гіпертексту влаштована всесвітня інформаційна мережа Internet, за допомогою якої вже зараз проводится так зване "дистанціоне навчання" - коли професори престижних університетів виступають з лекціями і відповідають на питання не звичної студентської аудиторії, а перед тими, хто в цей момент підключен до їх вузлу мережи. Недивлячись на тишу і візуальну відстутність слухачів, яких може бути не менше, чим глядачів у телеекрана, але на відміну від книги чи телепередачі зберігається зворотній зв’язок між викладачем і учнями. Це - реальність сьогоднішнього дня. Цікаво, що нас (і наших дітей) чекає в недалекому третьому тисячолітті.
Широке впровадження в навчальний процес нових інформаційних технологій відкриває широкі перспективи щодо поглиблення і розширення теоретичної бази знань, надання результатам навчання практичного значення, активізації пізнавальної діяльності, створення умов для повного розкриття творчого потенціалу учнів з урахуванням вікових особливостей, індивідуальних нахилів.
На сьогодні розроблено значну кількість програмних засобів, що дозволяють розв’язувати за допомогою комп’ютера досить широке коло математичних задач різних рівнів складності. Це такі програми як DERIVE, EURIKA, GRAN1, Maple, MathCad. Причому одні з цих програм розраховані на фахівців досить високої кваліфікації в галузі математики, інші - на учнів середніх навчальних закладів та студентів.
Можливість провести необхідний чисельний експеримент, швидко виконати потрібні обчислення чи графічні побудови, перевірити ту чи іншу гіпотезу, випробувати той чи інший метод розв’язування з?