Реферат: Понятие сплошной среды

Экспериментальные данные показывают, что большинство сред обладает специфическим свойством: отсутствием или малостью касательных напряжений pSt, т.е. вектор _S можно считать перпендикулярным любой площадке взаимодействия dS и равным нормальному напряжению pSn. Среду, обладающую таким свойством называют идеальной жидкостью или идеальным газом. Близки к таковым обычные воздух и вода при малых скоростях.

Указанное свойство для любой площадки с нормалью можно выразить соотношением, вытекающим из (2.1):

,

где –p – общее значение скалярных произведений. Величину p называют давлением. Его особенность заключается в независимости от направления рассматриваемого взаимодействия частиц. При p > 0 среда, как показывает опыт, находится в сжатом состоянии, поэтому и использован знак минус. Таким образом, матрица компонент тензора внутренних напряжений в идеальной жидкости (газе) имеет вид:

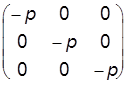, (2.6)

и тензор P целиком определяется скаляром p.

Понятно, что идеальная жидкость не единственно возможная модель сплошной среды, позволяющая определить компоненты тензора внутренних напряжений. Можно, например, рассматривать его компоненты как функции от деформации частицы: в этом случае среда называется упругой. В частном случае линейности это соотношение приобретает вид закона Гука. Изучением таких сред занимается теория упругости.

Особое место в механике сплошной среды занимает модель вязкой жидкости, предполагающая связь тензора внутренних напряжений с частными производными скорости по координатам. Имеется в виду эффект "трения" слоев вязкой жидкости между собой при наличии разности их поступательных скоростей.

3.1. Уравнение Навье-Стокса

В частном случае линейности связь представляется в виде закона Навье-Стокса (или обобщенного закона вязкости Ньютона):

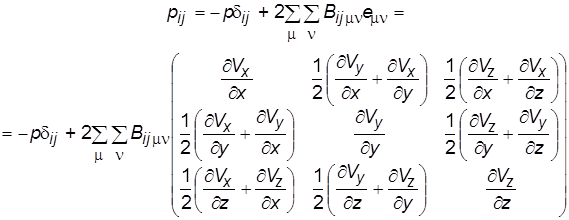, (2.7)

где – элементы единичной матрицы (с единицами на главной диагонали и нулями на всех остальных местах), матрица размерности 3´3, обозначенная emn, называется тензором скоростей деформации, а тензорный коэффициент линейности Bijmn описывает свойства вязкой жидкости.

Если свойства среды в разных направлениях одинаковы, то она называется изотропной, в противном случае – анизотропной. В изотропной среде Bijmn представляется симметричной матрицей размерности 3´3´3´3, одинаковой в любой системе координат. Можно показать [1], что в этом случае все компоненты тензора Bijmn выражаются всего лишь через два независимых параметра l и m, называемых коэффициентами Ламе, поэтому закон Навье-Стокса для вязкой изотропной жидкости имеет вид:

. (2.8)

4. Силы, действующие в атмосфере.

Силы, действующие в атмосфере делятся на массовые и поверхностные:

Массовые или объемные силы.

К массовым силам относятся те силы, которые действуют на каждый элементарный объем воздуха, и обычно, рассчитываются на единицу массы. К ним относятся:

Сила тяжести представляет собой векторную сумму двух сил: силы земного притяжения, направленной к центру Земли, и центробежной силы, возникающая из-за вращения Земли вокруг своей оси и направленная по радиусу круга широты, проходящей через рассматриваемую точку.

Сила Кориолиса (отклоняющая сила вращения земли) связана с вращением Земли вокруг своей оси и действует на движущиеся относительно Земли частицы воздуха (на воздушные течения атмосферы). Сила Кориолиса возникает в результате переносного вращательного движения Земли и одновременного движения частиц воздуха относительно земной поверхности.

или .

где ω – угловая скорость вращения Земли.

Применяя формулы векторного анализа получим составляющие силы Кориолиса по осям координат.

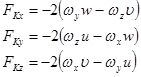
Поверхностные силы. К поверхностным силам относятся те силы, которые действуют на соприкасающиеся поверхности слоя воздуха.

Сила давления (сила барического градиента) возникает за счет неравномерного распределения давления. Вектор силы барического градиента определяется соотношением

,

а его составляющие, отнесенные к единице массы, по осям координат, имеют следующий вид:

, ,