Реферат: Постулаты квантовой механики

однозначными

непрерывными

конечными

нормированными.

2.1.6. Из формулы нормировки (2.3) следует размерность волновой функции стационарной системы в рассматриваемой задаче, а именно:

,

где размерность объема конфигурационного пространства равна произведению размерностей всех пространственных переменных, образующих его:

2.1.7. Выше говорилось об ортогональных наборах собственных функций эрмитовых операторов. Накладывая на каждую из них условие нормировки, приходим к чрезвычайно удобным ортонормированным наборам функций, например:

,

где

Эти два качества можно объединить в одно условие:

(2.4)

где – символ Кронекера, который может принимать два значения:

при и при .

Читатель, вероятно, догадался, что в нашем распоряжении появился мощный аппарат, подобный векторному.

2.2. Постулат 2. Операторы динамических переменных

2.2.1. Возможные значения физически наблюдаемых величин являются собственными значениями операторных уравнений вида

Каждой динамической переменной ставится в соответствие свой линейный самосопряженный оператор.

2.2.2. Важнейшими динамическими характеристиками одной частицы являются:

- радиус-вектор , где координаты могут быть:

декартовыми или полярными ( - углы, а – длина вектора);

- вектор импульса и его координаты – проекции;

- вектор момента импульса , являющийся векторным произведением радиуса-вектора на импульс

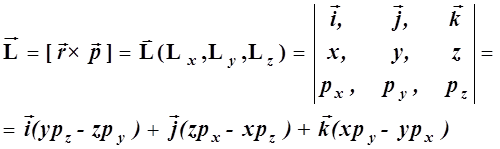(2.5)

и, соответственно, его проекции равны

(2.6)

(2.7)