Реферат: Постулаты квантовой механики

- кинетическая энергия Т, скалярная величина, которая в поступательном движении связана и с массой и импульсом

;

для одномерного вращения вокруг оси (например, z ) справедлива подобная же формула, где масса заменена моментом инерции I_z , а импульс – его моментом :

- потенциальная энергия, т.е. скалярное силовое поле, задаваемое функци-ей координат , в котором движется частица;

- полная энергия Е, равная сумме кинетической и потенциальной энергий

2.2.3. С учетом общих требований, предъявляемых к операторам квинтовой механики, постулируются простейшие операторы, а именно: операторы координат, определяющие положение частицы, и импульса ее,

- оператор координаты совпадает с умножением на саму координату q, т.е.: , или угол,

или, в общем виде ;

- оператор импульса имеет дифференциальную форму

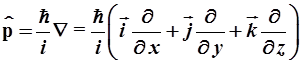(2.9)

где постоянная Планка Дж·с, и операторы координат импульса соответственно равны:

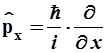, , (2.10)

Введение в оператор, мнимой единицы превращает его в самосопряженный т.е. отвечающий условию (1.5).

2.2.4. Остальные операторы строятся по формулам классической механики, где вместо координат и импульсов используются их операторы, Это утверждение можно считать следствием макроскопического устройства приборов по законам классической физики. Построим операторы и для одной частицы:

- операторы момента импульса и его проекций:

, (2.11)

, (2.12)

, (2.13)

(2.14)

В полярных координатах (например, сферических) соответствующие производные декартовых координат следует заменить их выражениями через полярные переменные;

- оператор кинетической энергии в декартовых координатах:

(2.15)

Переходя к полярным координатам, лапласиан преобразуют к ним. Для случая вращения по поверхности без радиальной компоненты движения, как это имеет место при вращении двухатомной молекулы вокруг центра масс, можно записать:

(2.16)

оператор потенциальной энергии, подобно координате, дается просто умножением на функцию потенциальной энергии, т.е.

, или (2.17)

оператор полной энергии называют гамильтонианом, в честь английского ученого Гамильтона, оставившего фундаментальные труды в механике, астрономии и математике, и обозначают его

(2.18)