Из формулы имеем . Интегрируя левую часть в пределах от 0 до , а правую - в пределах от 0 до t, найдем ,

или .

Вторично интегрируя, найдем отсюда закон равнопеременного вращения

.

Если величины и имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.

Скорости и ускорения точек вращающегося тела

Установив характеристики движения всего тела в целом, перейдем к изучению движения отдельных его точек.

1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см.рис.9). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время dt происходит элементарный поворот тела на угол , то точка М при этом совершает вдоль своей траектории элементарное перемещение . Тогда числовое значение скорости точки будет равно отношению ds к dt, т.е

или .

Скорость в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.

Таким образом, числовое значение скорости тонки вращающегося. твердого тела равно произведению угловой скорости тела на. расстояние от этой точки до оси вращения.

Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.

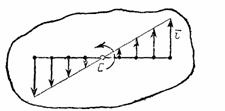
Так как для всех точек тела имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.

Рис.11	Рис. 12

Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами , .

В нашем случае =h. Подставляя значение v в выражения и аn , получим:

или окончательно:

, .

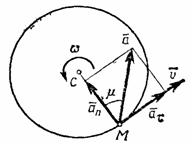
Касательная составляющая ускорения направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при, замедленном); нормальная составляющая всегда направлена по радиусу МС к оси вращения (рис. 12). Полное ускорение точки М будет или .

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом , который вычисляется по формуле . Подставляя сюда зна­чения и , получаем

Так как w и имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.14.

Рис 13	Рис 14

2. Векторы скорости и ускорения точек тела. Чтобы найти выражения непосредственно для векторов v и а, проведем из произвольной точки О оси АВ радиус-вектор r точки М (рис. 14). Тогда h=r sin а и по формуле

или .

Таким образом, модуль векторного произведения равен модулю скорости точки М.

Направления векторов и v тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерности их одинаковы. Следовательно, - формула Эйлера, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.

Момент силы относительно точки

Момент силы (синонимы: крутящий момент; вращательный момент; вертящий момент; вращающий момент ) — векторная физическая величина , равная произведению радиус-вектора проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Момент силы

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр , хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы , массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние, до оси вращения которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние, до оси вращения которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:

где — сила, действующая на частицу, а — радиус-вектор частицы.