Реферат: Практические задачи по ТОУЭС
К – критические операции
Продолжительность критического пути: 8 + 6 + 4 + 6 + 3 = 27
2. Оценить с достоверностью 90% оптимистичный
и пессимистичный срок завершения работ.
| Эксперты | |||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 6 | 7 | 6 | 5 | 4 | 4 | 4 | 5 | 6 | 6 | 6 | 4 | 4 | 8 | 10 | 3 | 4 | 4 | 5 | 6 |
Упорядочиваем по возрастанию:
10, 8, 7, 6, 6, 6, 6, 6, 6, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 3
Отбрасываем первые два значения и находим Qопт :
Qопт = 89 / 18 = 4,94
Упорядочиваем по убыванию и аналогично находим Qпес :
Qпес = 100 / 18 = 5,55
Находим Qср :
Qср = 107 / 20 = 5,35
Отклонение Qопт от Qср – 7,6%; Qпес от Qср – 3,7%. Оба значения в пределах 10%, таким образом достоверность 90% обеспечена.
3. Рассчитать требуемое количество экспертов, при котором влияние
1 эксперта на среднюю оценку составляет не более x = 9%.
Пробная оценка x + 1 экспертов:
6, 7, 6, 5, 4, 4, 4, 5, 6, 6
х = 9% => 0,91 £ E £ 1,09
Qср = 53 / 10 = 5,3
b = 10
T = ![]()
Таким образом, 9 человек – требуемое количество экспертов для проведения групповой оценки с влиянием одного эксперта не более 9%.
4. Проверить оптимальность указанных планов
f (x) = 3 x1 + 2 x2 – 4 x3 +5 x4 –> max
3 x1 + 2 x2 + 2 x3 – 2 x4 ³ -1
2 x1 + 2 x2 + 3 x3 – x4 ³ -1
x1 ³ 0 x2 ³ 0
x3 ³ 0 x4 ³ 0
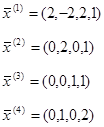
Координаты вектора x(1) не соответствуют ограничениям, т .к. х2 < 0
Остальные векторы подставляем в систему неравенств:
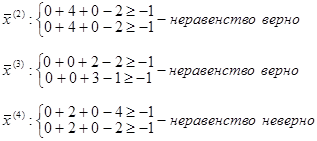
Таким образом, вектор х (4) тоже не удовлетворяет условиям. Вычисляем значения f(x):
x(2) : f (x) = 0 + 4 – 0 + 5 = 9
--> ЧИТАТЬ ПОЛНОСТЬЮ <--