Реферат: Пределы

2.Обратная величина б.м. есть б.б. Обратная величина б.б. есть б.м. lim Xn=¥ (n®¥) – б.б. Yn=1/Xn – б.м. Из lim Xn=¥ => M=1/E $N₀ , n>N₀ |Xn|>M =>n>N₀ .

|Yn|=1/|Xn|<1/M=E =>Yn – б.м. => lim Yn=0 (n®¥).

3.Сумма б.б величины и ограниченной есть б.б. величина.

Основные теоремы о пределах:

1. lim Xn=a, lim Yn=b => lim (Xn±Yn)=a±b (n®¥)

Док-во:lim Xn=a => Xn=a+a_n ; lim Yn=b => Yn=b+b_n ;

Xn ± Yn = (a + a_n ) ± (b + b_n ) = (a ± b) + (a_n ± b_n ) => lim(Xn±Yn)=a±b (n®¥).

2. limXnYn = lim Xn * lim Yn (n®¥).

3. lim Xn=a, lim Yn=b (n®¥) => lim Xn/Yn =
(lim Xn)/(lim Yn) = a/b.

Док-во:Xn/Yn – a/b = (a+a_n )/(b+b_n ) – a/b = (ab+a_n b–ab–ab_n )/b(b+b_n ) =(ba_n -ab_n )/b(b+b_n )=g_n => Xn/Yn=a/b+g_n => $ lim Xn/Yn = a/b = (lim Xn)/(lim Yn) (n®¥).

Пределы ф-ии непрерывного аргумента.

Число А наз-ся пределом ф-ии y=f(x) при х®x₀ , если для любого Е>0 сколь угодно малого сущ-ет такое число d>0, что при "x будет выпол |x-x₀ |<d, будет выполняться нер-во |f(x) – A|<E или "x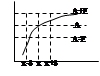 выпол x₀ -d<x<x+d=> A-E<f(x)<A+E.

Lim _{x ® x0} f(x)=A

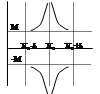Ф-ия y=f(x)наз-ся бесконечно большой при x ® x₀ если для "М>0 сколь угодно большого $d>0, что "x |x-x₀ |<d будет выполняться нер-во |f(x)|>M, "x x₀ -d<x<x₀ +d, -M>f(x)>M.

Lim f(x)= ¥ (x ® x₀ ).

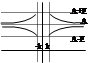Число А наз-ся пределом y=f(x) x ® ¥ , если для любого Е>0 можно найти число К, "x |x|>K |f(x)-A|<E.

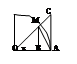
I замечательный предел.

Рассмотрим окр-ть радиуса 1; обозн угол МОВ через Х.

S_треуг МОА< S_сект МОА<S_треуг СОА.

S_треуг МОА=0,5ОА*МВ=0,5*1*sin=0.5sinX.

S_сект МОА=0,5*ОА*АМ=0,5*1*х=0,5х.

S_треуг СОА=0,5*ОА*АС=0,5*1*tgX=0,5tgX.

SinX<x<tgX {разделим все члены на sinX}

1<x/sinX<1/cosX или 1>(sinX)/x>cosX.

Lim cosX=1, lim 1=1 (x®0) =>lim (sinX)/x=1.

Следствия:

1. lim_{x ® 0} (tgX)/x=lim(sinX)/x*1/cosX=

=lim(sinX)/x*lim (1/cosX)=1;

2.lim_{x ® 0} (arcsinX)/x={arcsinX=t,sint=x,t®0}=

=lim_{t ® 0} t/sint=1;