Реферат: Пределы
2.Пусть фун y=f(x) непрерывна на отрезке [а,в] и на концах отрезка принимает значения разных знаков, тогда м/у точками а и в найдется по крайней мере одна точка х=с, в которой фун обращается в нуль: f(с)=0, а<с<в.
3.Пусть фун y=f(x) определена и непрерывна на отрезке [а,в]. Если на концах этого отрезка фун принимает значения f(а)=А, f(в)=В, то каово бы ни было число m, заключенное м/у А и В, найдется такая точка х=с, заключ м/у а и в, что f(с)=m.
Производная.
1.Пусть y=f(x), xÎX, x0 ; x0 +Dx ÎX => Dy=Df(x0 )=f(x0 +Dx)-f(x0 ), Dy/Dx=(f(x0 +Dx)-f(x0 ))/Dx.
Если $ limDx ®0 Dy/Dx, то этот предел наз-ся производн ф-ии в т-ке Х0 . · Если f(x) имеет производ в кажд т-ке xÎX, то мы можем брать прозвол Х, считая его фиксир, х+DхÎХ. LimDх ®0 (f(x0 +Dx)-f(x0 ))/Dx= =f/ (х)=df(x)/dx=dy/dx=y| (x).
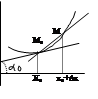2. Геометр смысл производ.
Производная фун f(x) в точке х0 равна угловому коэф-ту касательной к гр-ку фун f(x) в точке М (х0 ; f(x0 )).
Если т-ка М будет приближ-ся к т-ке М0 (при Dх®0), то секущая приближ-ся к касат.
y| (x0 )=limD х ® 0 (f(x0 +Dx)-f(x0 ))/ /Dx=limD х ® 0 Dy/Dx=limD х ® 0 tga==lima ® a 0 tga=tga0 .
L: y-f(x0 )=f\ (x0 )(x-x0 )
Nl =y-f(x0 )=-(x-x0 )/f\ (x0 ).
3. Основ теоремы о производных.
1. y=U(x)+V(x), y| =U| (x)+ V| (x) . Док-во: для х+Dх имеем: y+Dy=(u+Du)+(v+Dv). Следовательно, Dy=Du+Dv, Dy/Dx=Du/Dx+Dv/Dx, y| =limD x ® 0 Dy/Dx = limD x ® 0 Du/Dx+ limD x ® 0 Dv/Dx=U| (x)+V/ (x).
2. y=uv, y| =u| v+uv| . Док-во: y+Dy=(u+Du)(v+Dv), Dy=(u+Du)(v+Dv)-uv=Duv+uDv+DuDv, Dy/Dx=Duv/Dx+Dvu/Dx+DuDv/Dx,
y| = limD x ® 0 Dy/Dx= limD x ® 0 Duv/Dx + limD x ® 0 Dvu/Dx + limD x ® 0 DuDv/Dx={ limD x ® 0 Du=0, т.к ф-ия дифф-ма и непрерывна}=u| v+uv| .
3. y=u/v, y| =(u| v-uv| )/v2 . Док-во: y+Dy=(u+Du)/(v+Dv), Dy=(u+Du)/(v+Dv)-u/v=(vDu-uDv)/v(v+Dv)
Dy/Dx...
4. y=ax , y| =ax ln a. Док-во: ln y=x ln a, y| /y=ln a, y| =yln a y| =ax ln a.
Неявно задан фун и нахождение ее производ.
Говорят, что соот-е F(x;y)=0 задается неявно, если сущ фун у=f(x), х принадлежит отрезку [а,в] и, если подстав-е в F(x;y)=0 соот-е обращает его в тождество(º)· {F(x;y)=0,$у=f(x),х принадлежит отрезку [а,в],F(x;f(x)) º0}
Правило нахождения: Если F(x;y)=0 задает фцн неявно, т.е это будет тождество, то тождественное равенство можно по членно продифференцировать. {[F(x;y)]/ =0/ }
Формула Лейбница.
y( n ) =(uv)(n) =(u)(n) v+nu(n-1) v| +([n(n-1)]/[1*2])*n(n-2) v|| +…+uv(n)
Дифференцирование ф-ии в точке.
Ф-ия y=f(x) наз-ся дифференцируемой в т-ке Х0 , если Dy=ADx+O(Dx), где А не зависит от DХ, О(DХ) – б.м., более высокого порядка малости, чем DХ, когда DХ®0, т.е. limD x ® 0 O(Dx)/Dx=0. АDХ – главная часть приращения.
Теорема : y=f(x) дифф-ма в т-ке Х0 т и тт, когда она в этой т-ке имеет конечную производную A=f\ (x0 ).
Необход усл-ие дифф-ти: если ф-ия дифф-ма, то она имеет кон производ. Дано: Dy=ADx+O(Dx)
f\ (x0 )=limDx ®0 Dy/Dx= limDx ®0 [(ADx+O(Dx))/Dx] = limDx ®0 (A+O(Dx)/Dx)=A => Dy=f\ (x0 )Dx+O(Dx) => limDx ®0 Dy=0 => f(x) – непрерывна.
Достат усл-ие дифф-ти: если ф-ия в заданной т-ке имеет кон производ, то она дифф-ма. Дано: $f\ (x0 ) – число, f\ (x0 )=limDx ®0 Dy/Dx => Dy/Dx=f\ (x0 )+a(Dx) {a(Dч) – б.м.}, Dy=f\ (x0 )Dx+a(Dx)Dx => Dy=f\ (x0 )Dx+O(Dx), т.е. O(Dx)=a(Dx)Dx => limDx ®0 O(Dx)/Dx=limDx ®0 a(Dx)=0. Дифференциал ф-ии это главная часть приращения, линейная относит DХ.
Приближ знач ф-ии в некот т-ке: Dy=f(x0 +Dx)-f(x0 ) =>f(x0 +Dx)=f(x0 )+Dy»f(x0 )+df(x0 )=f(x0 )+f\ (x0 )dx, dx=Dx.