Реферат: Приближенное вычисление определенного интеграла при помощи квадратурной формулы Чебышева

. . . . . . . . . . . . . . . .

f(xn)=a0+a1xn+a2xn2+a3xn3+...+anxnn

получим формулу Чебышева.

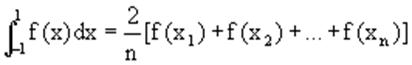
Значения х1,х2,..,хn для различных n приведены в таблице 3.

Таблица 3 – Значения х1,х2,..,хn для различных n.

n	I	ti	n	i	ti
2	1;2	± 0,577350	6	1;6	± 0,866247
3	1;3	± 0,707107	2;5	± 0,422519
2	0	3;4	± 0,266635
4	1;4	± 0,794654	7	1;7	± 0,883862
2;3	± 0,187592	2;6	± 0,529657
5	1;5	± 0,832498	3;5	± 0,321912
2;4	± 0,374541	4	0
3	0

2. Решение контрольного примера

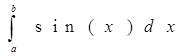
где a=0 ; b= ; при n=5;

f(x) = sin(x);

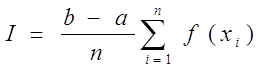
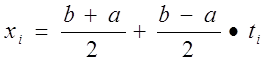
i	xi	yi
1	0,131489	0,131118
2	0,490985	0,471494
3	0,785	0,706825
4	0,509015	0,487317
5	0,868511	0,763367

x1= p/4+p/4*t1=p/4+p/4(-0,832498)=0,131489

x2= p/4+p/4*t2=p/4+p/4(-0,374341)=0,490985

x3= p/4+p/4*t3=p/4+p/4*0=0,785

x4=1- x2=1-0,490985 = 0,509015

x5=1- x1=1-0,131489=0,868511

y1=sin(x1) = sin(0,131489)=0,131118

y2=sin(x2) = sin(0,490985)=0,471494

y3=sin(x3) = sin(0,785)=0,706825

y4=sin(x4) = sin(0,509015)=0,487317

y5=sin(x5) = sin(0,868511)=0,763367

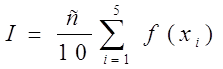
I = p/10(0,131118+0,471494+0,706825+0,487317+0,763367) =

=p/10*2,560121=0,8038779.

3. Описание программы Integral. pas. Алгоритм.

Процедура VVOD - заполняет массив, содержащий в себе аргументы xi

Процедура FORM - используя массив, содержащий аргументы xi заполняет массив yi

Процедура CHEB - используя массивы xi и yi, высчитывает по квадратурной формуле Чебышева приближенное значение интеграла.