Реферат: Принцип Максимума Понтрягина
легко выписывается в явном виде 
где С, D - постоянные.
Очевидно, что максимум функции Н по и
U достигается при
Таким образом, оптимальное управление и может принимать лишь два значения + 1 .
2 .Определить управление u(t) , которое дает минимум интегралу
, в процессе, описываемом уравнением 
(1).
Решение.
Введем дополнительную переменную
(2)
Для этой переменной имеем дифференциальное уравнение 
(
(3)
с начальными условиями, получаемыми из (2), т.е. х2 (0)=0. Минимизирующий функционал, используя (2), можно записать в виде I[T]=x2(T).
Построим функцию Гамильтона
Запишем сопряженную систему 
(3)
Запишем 
Y1 (Т)=0 (т.к. с1=0)
Y2 (Т)=-1
Из 
поэтому Y2 (е)=-1. Теперь функция Гамильтона запишется в виде H=-aY1x1+ Y1u-0,5x1 2 -0,5u 2 .
По принципу максимума функция Н при фиксированных х1 и Y1 достигает максимума по u : 
, 
, откуда 
.
Осталось решить систему уравнений (2) и (3) при условии , Y2 (Т)=-1,
, 
с граничными условиями 
Сведем данную систему к одному уравнению относительно U.
Добавим к этому уравнению граничные условия 
и решим его. Составим характеристическое уравнение к2 - (а2 +1) =0, к1,2=+(-) 
Найдем С1 и С2. 
С2 =-с2 е
. Тогда 
Используя граничные условия найдем С2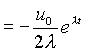 
Таким образом, определено оптимальное решение
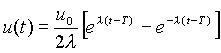
Примеры применения принципа максимума.
1. Простейшая задача оптимального быстродействия.
Пусть точка движется по прямой в соответствии с законом
(3.1)
где х - координата. Требуется найти управление и, переводящее точку из начального положения в начало координат за минимальное время Т (задача оптимального быстродействия). При этом скорость точки в конце траектории должна быть нулевой, а управление - удовлетворять условию
.
Применим к сформулированной задаче принцип максимума Понтрягина . Введем фазовые переменные 
. Тогда движение управляемого объекта описывается системой двух дифференциальных уравнений первого порядка:
(3.2)
Начальное положение
при t0 =0 и конечное положение (0, 0) фиксированы, а конечный момент времени Т не фиксирован.
В обозначениях п.п. 1, 2 в данной задаче U ==[- 1, 1], f0 =1, Ф=0, а функция Гамильтона имеет вид
Общее решение сопряженной системы
легко выписывается в явном виде
где С, D - постоянные.
Очевидно, что максимум функции Н по и U достигается при
Таким образом, оптимальное управление и может принимать лишь два значения + 1 .
2 .Определить управление u(t) , которое дает минимум интегралу
, в процессе, описываемом уравнением (1).
Решение.
Введем дополнительную переменную
(2)
Для этой переменной имеем дифференциальное уравнение ( (3)
с начальными условиями, получаемыми из (2), т.е. х2 (0)=0. Минимизирующий функционал, используя (2), можно записать в виде I[T]=x2(T).
Построим функцию Гамильтона
Запишем сопряженную систему (3)
Запишем
Y1 (Т)=0 (т.к. с1=0)
Y2 (Т)=-1
Из поэтому Y2 (е)=-1. Теперь функция Гамильтона запишется в виде H=-aY1x1+ Y1u-0,5x1 2 -0,5u 2 .
По принципу максимума функция Н при фиксированных х1 и Y1 достигает максимума по u : , , откуда .
Осталось решить систему уравнений (2) и (3) при условии , Y2 (Т)=-1,
, с граничными условиями
Сведем данную систему к одному уравнению относительно U.
Добавим к этому уравнению граничные условия и решим его. Составим характеристическое уравнение к2 - (а2 +1) =0, к1,2=+(-)
Найдем С1 и С2. С2 =-с2 е. Тогда
Используя граничные условия найдем С2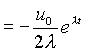
Таким образом, определено оптимальное решение
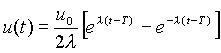
О методах решения задач оптимального управления
Убедимся вначале, что необходимые условия оптимальности в форме принципа максимума дают, вообще говоря, достаточную информацию для решения задачи оптимального управления (2.1), (2.2).
Условие максимума (2.4) позволяет, в принципе, найти управление и как функцию параметров х, t, 
(2.7)
Рассмотрим систему дифференциальных уравнений
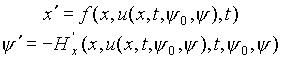(2.8)
объединяющюю систему уравнений движения объекта и сопряженную систему.
Как известно, общее решение системы (2.8), состоящей из 2n обыкновенных дифференциальных уравнений первого порядка, зависит от 2п параметров. Кроме того, система необходимых условий оптимальности содержит т параметров
и параметр y0 . Таким образом, общее число неизвестных равно 2n+m+1.
Для их определения мы имеем 2п условий (2.5), (2.6) и т условий (2.2). Еще одно условие определяется из следующих соображений.
Легко понять, что, в силу линейности функции Н по переменным принцип максимума Понтрягина определяет вектор () с точностью до положительного постоянного множителя. Поэтому если в конкретной задаче удается показать, что 
, то полагают обычно 
== - 1. В противном случае накладывают какое-либо условие нормировки, например, 
Таким образом, общее число условий равно 2n+m+1 и совпадает с числом неизвестных параметров, что, в принципе, позволяет определить эти параметры. Изложенные соображения дают возможность в простейших случаях решить задачу оптимального управления в явном виде.
Опишем численный метод, основанный на тех же соображениях. Для этого рассмотрим краевую задачу для системы дифференциальных уравнений (2.8) с краевыми условиями (2.5), (2.6), а также выписанными на основе (2.2) краевыми условиями