Реферат: Природа рокового цикла Сепкоски - Мюллера - Роде
Косарев А.В.
Исследование группы учёных из Калифорнийского университета, опубликованное в мартовском выпуске журнала Nature за 2005 год, проводивших “анализ остатков ископаемых свидетельствует о том, что циклический процесс массового исчезновения видов на Земле повторяются каждые 62 млн. лет с точностью плюс-минус 3 млн. лет. Последний раз событие этого ряда – гибель динозавров. “У нас не осталось сомнений в наличии данного цикла, говорит профессор Джеймс Кишнер (James Kirchner), который уже много лет занимается этой проблемой. – Хуже всего то, что мы до сих пор не можем установить причину катастроф, которые в прошлом приводили к массовой гибели динозавров и тысяч иных видов животных. Совершённое открытие – удивительное, неожиданное и необъяснимое”. Ричард Мюллер (Richard Muller) и его ученик Роберт Роде (Robert Rohde), авторы опубликованной в Nature статьи, выдвигают следующие возможные гипотезы. Во-первых, полагают они, периодическое прохождение Солнечной системы через одно из облаков газа в Галактике может вызывать резкие климатические изменения на Земле, несовместимые с существованием некоторых видов, сформировавшихся в других условиях. Во-вторых, Ричард Мюллер ещё двадцать лет назад предположил, что у Солнца может существовать спутник – карликовая звезда, которой он дал имя “Немезида”. Каждые 62 млн. лет она приближается к нам на расстояние, достаточное, чтобы возмутить орбиты комет во внешней части Солнечной системы, так называемом облаке Оорта, и направить их во внутренние области Солнечной системы, подвергая нашу планету настоящей “бомбардировке”. Правда, здесь тоже возникает множество сомнений – расчёты показали, что существование двойной системы с таким большим орбитальным периодом будет нестабильным. Согласно третьей гипотезе возможно наличие геофизического механизма неизвестной пока природы, периодически порождающего всплеск вулканической активности на Земле. Массовый выброс пепла может вызвать резкое и длительное снижение температуры со всеми вытекающими отсюда последствиями.
В своём исследовании учёные использовали список морских ископаемых организмов объёмом 560 страниц, составленный 14 лет назад известным палеобиологом из Чикагского университета Дж. Джоном Сепкоски - младшим (J. John Sepkoski Jr.). В них сам Сепкоски полагал, что цикличность развития морских организмов повторяется с периодичностью 26 млн. лет. Мюллер и Роде показали, что цикл 62 млн. лет проявляется несравненно более чётко, хотя и они отметили признаки наличия циклов с периодичностью около 140 млн. лет.” [См. рис. 1]. Рисунок и изложенная выше информация получены автором из статьи: “Скорую гибель человечеству пророчат окаменелости?”, размещённую на сайте журнала C News.
Первая из прелагаемых выше гипотез не выдерживает критики по причине того, что Галактика вращается как единое целое, все входящие в неё компоненты вращаются практически с одинаковой угловой скоростью и периодом обращения вокруг центра Галактики равным 240-250 миллионов лет. Чтобы эта гипотеза работала необходимо иметь или четыре покоящихся на орбите Солнца вредоносных облака или это облако должно вращаться по орбите Солнца со скоростью строго в четыре раза меньшей, чем у Солнца. Цифра четыре появилась не случайно: если умножить 62 млн. лет на четыре, то получим 248 млн. лет, т.е. как раз период обращения Солнца вокруг центра Галактики. Отметим напрашивающуюся связь между периодом рокового цикла (62 млн. лет) и периодом обращения Солнца вокруг центра Галактики (240-250 млн. лет).
Недостатки второй гипотезы описаны выше. Что касается третьей гипотезы, то она представляется достаточно правдоподобной, но здесь необходима увязка данного механизма с периодическим движением Солнца вокруг центра Галактики. Трудно представить такую поразительную согласованность независимых процессов на столь огромных промежутках времени. В связи с этим заметим, что ещё в конце 19-го века французским геологом М. Бертраном было обращено внимание на совпадение длительности крупно масштабных тектонических циклов со временем обращения Земли и всей Солнечной системы по галактической орбите.
Существует множество гипотез и публикаций на подобную тему, особенно в связи с таинственной причиной гибели динозавров.
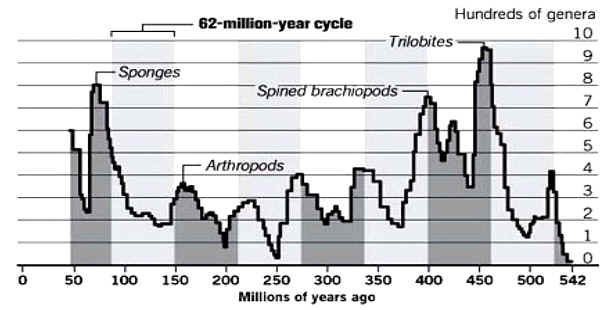
Рис.1
“Мы обязаны рассмотреть все мыслимые объяснения, чтобы понять причину этого таинственного и рокового цикла расцвета жизни на планете и последующей её гибели, считает г-н Мюллер. – Пока что это нам не удалось. И это нужно сделать немедля – хотя и не впадая при этом в панику”. [Л-4].
Предлагаем вниманию читателя гипотезу, которая как, представляется автору, достаточно просто объясняет эту, казалось бы, мистическую цикличность. Гипотеза исходит из уже установленных фактов и закономерностей космологии, геофизики и метеорологии. Она основывается на факте ячеистой структуры Вселенной и теории тектоники литосферных плит. Суть идеи.
Вещество во Вселенной располагается не хаотично, а формируется в ячеистые структуры, подобие куба, ребро которого имеет величину порядка 100-300 миллионов световых лет. Причём всё вещество располагается в тонком (по космологическим меркам) слое граней ячейки. Внутри ячейки вещества нет, поэтому в английской литературе ячейки называются void – пустой. Это дало повод астрофизикам образно сравнить ячеистую структуру Вселенной с пеной. Каждая вершина ячейки-куба является общей для восьми соседних ячеек, поэтому здесь сосредотачивается наибольшая плотность и масса вещества, формируются сверхскопления звёзд первой величины. Эти сверхскопления обладают огромными массами и создают соответствующие закону всемирного тяготения поля сил тяготения. Каждое ребро ячейки-куба является общим для четырёх соседних ячеек. Поэтому в рёбрах формируются сверхскопления второй (меньшей величины). И, наконец, сторона (грань) ячейки-куба является общей для двух ячеек, поэтому здесь формируются самые малые (третьей величины) сверхскопления. К одному из таких малых сверхскоплений и относится наша Галактика. Факт зарождения жизни на краю малого сверхскопления во многом связан с тем, что здесь существуют наиболее щадящие условия для жизни. Схема нашей ячейки, в плоскости грани которой, вращается наша Галактика, изображена (без масштаба) на рисунке 2. На Рис.2 цифрами 1, 2, 3 и 4 отмечены сверхскопления первой величины; латинскими буквами a, b, c, d отмечены сверхскопления второй величины; 5 – центр нашей Галактики; 6 – Солнце; 7 – круговая орбита вращения Солнца вокруг центра Галактики; 8 – внешняя граница нашей Галактики. При вращении Солнца по орбите вокруг центра Галактики, Солнечная система четыре раза за оборот, с периодичностью в 62 миллиона лет, сближается со сверхскоплениями первой величины и четыре раза со сверхскоплениями второй величины, испытывая каждый раз усиление гравитационного воздействия сверхскоплений.
Согласно базовой теории современной геофизики, теории тектоники литосферных плит, материки представляют собой огромные литосферные плиты способные под воздействием внешних сил совершать дрейф по Земной поверхности.
Так вот причиной рокового цикла Сепкоски – Мюллера – Роде являются приливные литосферные волны, возникающие под гравитационным воздействием сверхскоплений, в период сближения. Точно также как возникают приливные волны в мировом океане под гравитационным воздействием Луны. [См. например, [Л-3]].
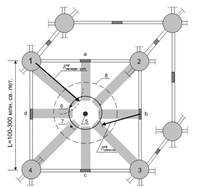
Рис.2
Произведём обоснование и количественные оценки выше изложенного.
Рассчитаем величину силы, необходимую для того, что бы вызвать подвижки Земной поверхности при приближении Солнечной системы к сверхскоплению. Предварительно напомним основные положения теории тектоники литосферных плит. “По астеносфере Земли перемещаются, как единый ансамбль (выделено автором), плиты литосферы – верхней, наиболее холодной, а поэтому твёрдой и хрупкой планетарной оболочки, включающей земную кору и часть мантии. Астеносфера – слой мантии, подстилающий литосферу и способный к вязкому или пластическому течению. Толщина литосферы меняется в широких пределах от единиц километров в рифтовых трещинах дна океана до 200 км. и более под древними щитами и платформами материков. Крупных литосферных плит немного – всего 8 – 10. … Эти плиты все вместе занимают более 85% площади земной поверхности”. [Л-6]. Для оценки величины силы примем в рассматриваемой задаче наиболее жёсткие условия - сухое трение или трение скольжения. Для того, что бы литосферная плита пришла в движение, необходимо превышение силы притяжения плиты к сверхскоплению над силой трения между литосферной плитой и подстилающей её мантией.
![]() (1)
(1)
Силу притяжения определим из закона всемирного тяготения Ньютона:
![]() (2)
(2)
В (2): ![]() [Л-8] – гравитационная постоянная;
[Л-8] – гравитационная постоянная;![]() - масса сверхскопления 1-й величины, равная
- масса сверхскопления 1-й величины, равная ![]() масс Солнца, [Л-9];
масс Солнца, [Л-9];
Масса Солнца равна ![]() [Л-8];
[Л-8]; ![]() - масса литосферной плиты;
- масса литосферной плиты; ![]() - расстояние от сверхскопления до Земли. Это расстояние определяем как расстояние от вершины до центра грани ячейки. Величину ребра ячейки принимаем в 200 млн. св. лет. Световой год равен
- расстояние от сверхскопления до Земли. Это расстояние определяем как расстояние от вершины до центра грани ячейки. Величину ребра ячейки принимаем в 200 млн. св. лет. Световой год равен ![]() [Л-8].
[Л-8].
Силу трения между плоскостью литосферной плиты и плоскостью подстилающей мантии определим по формуле: ![]() (3). [Л-7, формула 12.1]. В (3)
(3). [Л-7, формула 12.1]. В (3) ![]() - коэффициент трения. “Коэффициент трения
- коэффициент трения. “Коэффициент трения![]() , для умеренно жёстких поверхностей обычно меньший единицы.” [Л-7]. Учитывая, что мы делаем оценки в рамках космологических масштабов и точности, то даже в случае изменений коэффициента трения в рамках от 0.1 до 10, значение
, для умеренно жёстких поверхностей обычно меньший единицы.” [Л-7]. Учитывая, что мы делаем оценки в рамках космологических масштабов и точности, то даже в случае изменений коэффициента трения в рамках от 0.1 до 10, значение ![]() =1 является хорошим усреднением;
=1 является хорошим усреднением; ![]() - нормальная сила, равная весу литосферной плиты. Вес литосферной плиты определяем по закону Ньютона:
- нормальная сила, равная весу литосферной плиты. Вес литосферной плиты определяем по закону Ньютона:
![]() (4).
(4).
В (4) ![]() - масса Земли [Л-8];
- масса Земли [Л-8]; ![]() - радиус Земли [Л-8].
- радиус Земли [Л-8].
С учетом зависимостей (2), (3) и (4) запишем равенство (1). Равенство в (1) соответствует силе, с которой начинается подвижка литосферных плит.
![]()
![]() (5).
(5).
Отметим тот факт, что в (5) масса литосферной плиты стоит в обеих частях равенства и сокращается. Это означает, что момент начала подвижки плит не зависит от массы плит. Этим и объясняется движение литосферных плит как единого ансамбля. Правда, это возможно при условии, что коэффициенты трения у всех плит одинаковы. Конечно, коэффициент трения локально по поверхности подошвы плиты может меняться в широких пределах, в зависимости от местных условий. Но с учётом больших размеров литосферных плит усреднение по поверхности выравнивает коэффициенты трения для больших плит.
Исходя из (5) вычислим значение коэффициента трения. Посмотрим, насколько вычисленное значение будет соответствовать условиям сухого трения, когда коэффициент трения имеет значение близкое к единице.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--