Реферат: Проектирование кулачковых механизмов

Любую непрерывную дифференцируемую функцию вида можно представить разложением в ряд:

, (1)

. (2)

(1) - полиномиальное разложение;

(2) - разложение в тригонометрический ряд;

- остаточный член.

Двойное интегрирование выражений (1) и (2) позволяет получить

, (3)

, (4)

, (5)

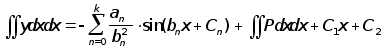, (6)

где С₁ , С₂ - константы интегрирования.

Если предположить что , то интегралы от Р из формул (3) ... (6) можно исключить. Таким образом, имея зависимости вида (1) или (2), легко получить аналитические зависимости вида (3) или (4) и зависимости вида (5) или (6).

В программе QUL реализован алгоритм, вычисляющий значения первого и второго интеграла относительного ускорения толкателя для определения углов поворота кулачка. Следует заметить что в общем виде может иметь точки разрыва. При этом функция при разбивается на участки

,

где - индекс участка (режима).

Так что функция - кусочно-непрерывная дифференцируемая функция в области своего определения , каждый - й участок называется режимом, при этом

Чтобы избежать неопределенности в задании функции , отрезки открыты справа. Для обеспечения задания функции на - ом режиме предполагается, что . Требование не является обязательным.

Точность интегрирования определяется не шагом по углу поворота, а точностью задания функции на участке, т.е. величиной .

Если исходная функция заданна в виде графика или таблицы значений, то решение получают при помощи численных или графических методов. Для определения передаточной функции скорости толкателя интегрируют заданную функцию ускорения толкателя, интегрируя полученную функцию скорости, находят функцию перемещения толкателя. Обычно применяется численное интегрирование методом трапеций по формулам:

где - приращение угла поворота кулачка на шаге интегрирования,

N - число равноотстоящих точек, в которых заданны значения переменной.

Примечание:

В течение цикла движения толкатель кулачкового механизма должен переместиться из начального положения на величину хода h , а затем возвратиться в исходное положение, то есть перемещение толкателя на фазе удаления равно перемещению на фазе сближения. Следовательно, график кинематической передаточной функции скорости должен удовлетворять условию:

,

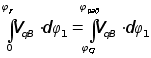где j_со -угловая координата начальной точки фазы сближения.