Реферат: Прогнозирование с учетом фактора старения информации

Интегральные функции n(T) и N(T), выраженные в абсолютных единицах измерения (квантах информации), можно выразить в относительных единицах, что позволит устранить искажающее воздействие динамики границы ретроспекции. С этой целью введем новую переменную m(T) , которая обозначает долю полезной информации в общем ее объеме при формировании прогнозного фона, достигнутую к моменту времени Т. По определению

(2.1)

При динамические характеристики m(T) совпадают с аналогичными характеристиками n(T).

Функция m(T) – монотонно возрастающая функция ретроспекции, изменяющаяся в интервале (0,1).

Когда n(Т) приближается к N( T) , то m(Т) стремится к едини­це асимптотически при. Это обстоятельство позволяет получить более простые аналитические зависимости для куму­лятивной функции, не искажая значительно реальной картины.

Для дальнейшей спецификации кумулятивной функции не­обходимо кроме интегральной функции рассмотреть и диффе­ренциальную, определив ее следующим образом

(2.2)

Тогда дифференциальная относительная кумулятивная функция будет иметь вид:

(2.3)

Требования к виду функций и вытекают из каче­ственного описания процесса. Эти функции всюду положитель­ные, к концу периода ретроспекции их значение монотонно убывает и стремится к нулю.

Поскольку процесс кумуляции ценной информации имеет верхний придел, то необходимо ввести в исследование переменную, характеризующую скорость приближения процесса к концу. Эта переменная будет определять темп старения информации. Она выражается в виде той части еще не учтенной полезной информации, которая может быть использована в прогнозной модели:

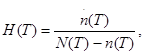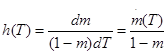или (2.4)

Интенсивность старения информации H(T) и h(T) определяет конкретную конфигурацию кривой h(T) или m(T).

Отсюда следует, что дифференциальное уравнение кумуляции информации (далее рассматриваются относительные функции) имеет вид:

(2.5)

Проинтегрировав это уравнение при естественных ранее введенных допущениях , получим уравнение для определения интегральной функции

(2.6)

Здесь предполагается, что m(0)-0, а

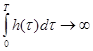при т.к.

Интенсивность старения информации в общем случае будет зависеть от самых различных факторов. Поэтому функция h(t) можно записать в следующем общем виде

h(T)=h(T,m(T),xi)

гдеxi – множествоэкзогенных факторов, определяющих конкретный процесс старения информации.

Здесь предполагается, что значения этих факторов явно не зависят от m(T), T .

Дальнейший анализ динамики процесса старения информации состоит в спецификации вида функции h, который необходимо проводить исходя из эмпирических соображений.

Для выявления тенденций использования информации в исследованиях получило распространение аналитическое выравнивание эмпирических рядов распределения с помощью различных функций, которые описывают полиномы и комуляты распределения квантов информации, получаемые при наблюдении. Традиционными моделями, описывающими старение науч­ной информации, являются кривые Бартона-Кеблера

(2.7)

или их модификации (Аврамеску, Коула)

, (2.8)

, и др . (2.9)

Анализ механизма старения информации по кривым Бартона-Кеблера позволяет умозрительно сделать вывод о том, что эти кривые соответствуют двум потокам научной информации, быстро стареющей и медленно стареющей, затухающей в два раза медленнее (по всей видимости второй поток относится к классическим и фундаментальным результатам). Применительно к исследуемой области это обстоятельство позволяет сделать вывод, что эти модели могут быть использованы в основном при применении системного анализа результатов фундамен­тальных исследований (см. табл. 3, приложение С).

Длительность существования полезной информации при прогнозировании в микроэкономике является величиной случайной и зависит от ряда факторов и может быть описана кривыми Гомперца или распределениями Гомперца-Макегама, в основе которых лежит идеализированная модель (экспоненциальное распределение)

, (2.10)

где - величина, обратная средней длительности жизненного цикла полезной информации.

Соотношению (2.10) соответствует пуассоновский поток событий, однако предположение о постоянстве параметра неприемлемо для широкого класса задач прогноза микроэкономических показателей, что обусловливает необходимость постулирования некоторых дополнительных предположений о вариации этого параметра. Модификация экспоненциальной зависимости (2.10) мож?