Реферат: Пространственно-временная метрика, уравнения геодезических. Ньютоново приближение

Выражение — векторная форма метрики в стандартных координатах Шварцшильда; соответствующую скалярную форму в сферических координатах, как строгое решение уравнений Эйнштейна, впервые получил в 1916 г. К. Шварцшильд.

Мы показали, что общее выражение (1.1.2) с помощью формул (1.1.3) и (1.1.4) может быть приведено к шварцшильдовой форме (1.1.12) путем чисто алгебраического преобразования соотношения (1.1.8). Таким образом, уравнения, выведенные с использованием метрики Шварцшильда, можно преобразовать к некоторой общей сферически симметричной метрике.

1.3 Изотропные координаты

Рассмотрим систему координат, определяемую формулой

В соответствии с (1.1.3), получаем

Дифференцируя (1.1.14) по, находим

Следовательно, по (1.1.4) имеем

или

и выражение (1.1.2) для элементапринимает вид

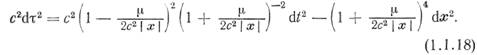
Это выражение известно как изотропная форма метрики Шварцшильда, поскольку, приняв в, можно найти, что координатная

скорость света в точке х, задаваемая формулой

одинакова во всех направлениях.

2. УРАВНЕНИЯ ГЕОДЕЗИЧЕСКИХ

Можно показать (см. Приложение В), что уравнения, определяющие геодезические, выводятся из обычных уравнений Эйлера — Лагранжа, которые в координатах Шварцшильда имеют вид

где— лагранжиан,

а точка сверху обозначает дифференцирование по

Уравнение (1.2.1) дает непосредственно