Реферат: Проводниковые материалы

g = K₀ ^2/3 l

(2-4)

где K — численный коэффициент; остальные обозначения — прежние.

Для различных металлов скорости хаотического теплового дви­жения электронов v _T (при определенной температуре) примерно оди­наковы. Незначительно различаются также и концентрации свобод­ных электронов п₀ (например, для меди и никеля это различие меньше 10 %). Поэтому значение удельной проводимости у (или удельного сопротивления r) в основном зависит от средней длины свободного пробега электронов в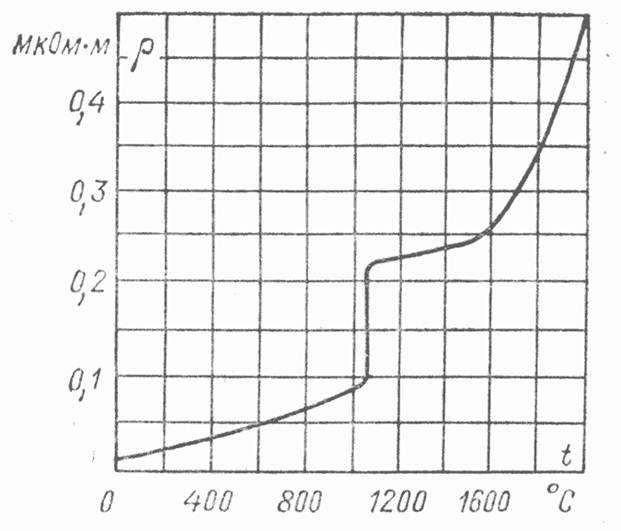

Рис. 2-1. Зависимость удельного сопротивления r меди от температуры

данном проводнике l, которая, в свою очередь, определяется структурой проводникового материала. Все чистые металлы с наиболее правильной кристаллической решеткой харак­теризуются наименьшими значениями удельного сопротивления; примеси, искажая решетку, приводят к увеличению r. К такому же выводу можно прийти, исходя из волновой природы электронов. Рассеяние электронных волн происходит на дефектах кристалличе­ской решетки, которые соизмеримы с расстоянием около четверти длины электронной волны. Нару­шения меньших размеров не вызы­вают заметного рассеяния волн. В металлическом проводнике, где длина волны электрона около 0,5 нм, микродефекты создают значительное рассеяние, уменьша­ющее подвижность электронов, и, следовательно, приводит к росту r материала.

Температурный коэффициент удельного сопротивления металлов. Число носителей заряда (концентрация свободных электронов) в металлическом проводнике при повышении температуры практически остается неизменным. Однако вследствие усиления колебаний узлов кристаллической ре­шетки с ростом температуры появляется все больше и больше препятствий на пути направленного движения свободных электронов под действием электрического поля, т. е. уменьшается средняя длина свободного пробега электрона l. уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов и возрастает удельное сопротивление (рис. 2-1). Иными словами, температурный коэффициент удельного сопротивления металлов, (кельвин в минус первой степени)

TKr =ar = (1/r) (d r/dT )

(2-5)

положителен. Согласно выводам электронной теории металлов значе­ния a_r ., чистых металлов в твердом состоянии должны быть близки к температурному коэффициенту расширения идеальных газов, т.е. 1/273»0,0037 К^-1 . При изменении температуры в узких диапазонах на практике допустима кусочно-линейная аппрокси­мация зависимости r (Т); в этом случае принимают, что

r2 = r1 [1+ar (T2 –T1 )]

(2-6)

где r₁ , и r₂ — удельные сопротивления проводникового материала при температурах Т₁ , и T₂ , соответственно (при этом T₂ > Т₁ );

a_r — так называемый средний температурный коэффициент удель­ного сопротивления данного материала в диапазоне температур от Т₁ , до Т₂ .

Изменение удельного сопротивления металлов при плавлении. При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления r, как это видно, например для меди, из рис. 2-1; однако у некоторых металлов r при плавлении уменьшается. Удельное сопротивление увеличивается при плавлении у тех метал­лов, у которых при плавлении увеличивается объем, т. е. уменьша­ется плотность; и, наоборот, у металлов, уменьшающих свой объем при плавлении, — галлия, висмута, сурьмы r уменьшается.

Удельное сопротивление сплавов. Как уже указывалось, примеси и нарушения правильной структуры ме­таллов увеличивают их удельное сопротивление. Значительное воз­растание r наблюдается при сплавлении двух металлов в том случае, если они образуют друг с другом твердый раствор, т. е. при (утвер­ждении совместно кристаллизуются, и атомы одного металла входят в кристаллическую решетку другого.

Теплопроводность металлов. За передачу теп­лоты через металл в основном ответственны те же свободные элект­роны, которые определяют и электропроводность металлов и число которых в единице объема металла весьма велико. Поэтому, как правило, коэффициент теплопроводности g_T металлов намного больше, чем коэффициент теплопроводности диэлектриков. Очевидно, что при прочих равных условиях, чем больше удельная электрическая проводимость у металла, тем больше должен быть и его коэффициент теплопроводности. Легко также видеть, что при по­вышении температуры, когда подвижность электронов в металле и соответственно его удельная проводимость g уменьшаются, отноше­ние коэффициента теплопроводности металла к его удельной про­водимости g_T /g должно возрастать. Математически это выражается законом Вчдемана—Франца—Лоренца:

gT /g = LoT

(2-7)

где Т —термодинамическая температура, К; Lo —число Лоренца, равное

Lo=(p2 k 2 )/(3e 2 )

(2-8)

Подставляя в формулу (2-8) значения постоянной Больцмана k = 1.38 ×10^-23 Дж/К и заряда электрона е = 1,6×10^-19 Кл, полу­чаем Lo = 2,45×10^-8 B² K² .

Термоэлектродвижущая сила. При соприкос­новении двух различных металлических проводников между ними возникает контактная разность потенциалов. Причина появления этой разности потенциалов за­ключается в различии значений работы выхода электронов из раз­личных металлов, а также в том, что концентрация электронов, а следовательно, и давление электронного газа у разных металлов и сплавов могут быть неодинаковыми. Из электронной тео­рии металлов следует, что контактная разность потенциалов между металлами А и В равна

UAB =UB - UA + (kT/e) ln (n0A /n0B )

(2-9)

где U_A и U_B — потенциалы соприкасающихся металлов; n_0A и n_0B — концентрации электронов в металлах А и В; k — постоянная Больцмана; e —абсолютная величина заряда электрона.

Если температуры «спаев» одинаковы, то сумма разности потен­циалов в замкнутой цепи равна нулю. Иначе обстоит дело, когда один из спаев имеет температуру T₁ , а другой —температуру Т₂ ( рис. 2-2).