Реферат: Quantization error analysis of the quadrature components of narrowband signals

The implementation of filters with digital circuits having finite word-length introduces unavoidable quantization errors. These effects have been widely studied [1–7]. The three common sources of quantization error are: input quantization, coefficient quantization and quantization in arithmetic operations. In [2–4, 6] papers the statistical characteristics of the quantization errors of scalar signals have been studied. The influence of all three sources of quantization errors on performance of a Chebyshev digital third-order highpass filter was investigated in [5] also for the scalar input signals. The quantization errors of complex input signals, which were represented by its inphase and quadrature components were studied in [7] to evaluate the performance of coder/decoders with phase shift keying. However, only computer simulation results were presented in this paper.

Usually digital signal processing of narrowband radio signals (i.e. signals for which inequality is valid) is carried out after the demodulation of the input signal into the quadrature components. Hence, our attention in this paper will be on input quantization of the complex signals. We adopt stochastic methods to analyse quantization errors [1–6]. The block diagram of the input narrowband signals converter, which produces the quadrature components of the signals and then transforms them into digital form is shown in fig. 1 (the left part of the plot).

Fig. 1. Block diagram of narrowband signals' converter

The converter contains two frequency mixtures, two low pass filters (LPF), two analog-to-digital converters (A/D) and a control unit. The quantizing (roundoff) errors of the inphase Xi and the quadrature Yi components are caused by limited bit representation of the code words of these components. To quantitatively evaluate these errors we will transform the quadrature components which have the roundoff errors into the narrowband signal again, and then we will estimate the amplitude and phase errors in this signal in comparison with the input one. For this purpose we will add in the block-diagram in fig. 1 the necessary blocks (the right part of the plot): digital-to-analogue converters (D/A), low pass filters (LPF) which restore the continuous analogue signal, frequency mixtures and adder. Assume all blocks work in ideal mode, don't introduce the delay, then the magnitude of the transfer function of the LPF is

If the Nyquist constraint is valid the values of the restored analogue quadrature components and (is the clock period) will be equal to the discrete values of quadrature components – and respectively.

Preliminaries

Let and be the inphase and quadrature components at the input of the A/D converters. At each sampling instant i, the quantized outputs and , the quantization (roundoff) errors and , and the input and are related by

, . (1)

Suppose roundoff errors are independent with zero mean, variance and uniform distribution in interval 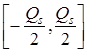, cf. [6]. is the step of quantizing.

If the input signal is a narrowband signal

,

then the output signal is also a narrowband signal and can be written in the form

(2)

where the values of and are given by formula (1).

The vector representation of the and signals is given in fig. 2. Obviously, we have

. (3)

Fig. 2. Vector representation of input and output (distorted) signals

Under the assumption about independent random variables and the hypothesis about uniform distribution of the random angles may be accepted. It is clear from the fig. 2 and formula (2) that the signal has a parathytic amplitude modulation as well as a phase modulation. The parathytic modulation is caused by the quantizing errors of the signal's quadrature components.

Amplitude error analysis of the quantized narrowband signals.

The variance of the magnitude is

where smax is the maximum available amplitude of the input signals of the A/D converter, n – is the number of bits of the A/D converter.

It is interesting to note that quantizing errors exist only when the input signals exists, nevertheless these errors are additive but not multiplicative because the values of these errors depend on the quantizing step , but do not depend on the amplitude of the input signal . (See formula (5)). We are interested in the amplitude and phase of the output signal . Let us find the statistical characteristics of the amplitude and phase.

The length of the vector can easily be found from the triangle OAB (see fig. 2)

, (6)

where .

--> ЧИТАТЬ ПОЛНОСТЬЮ <--