Реферат: Радиотехническая система передач

Теорема 1. Минимальное расстояние линейного кода равно минимальному весу ненулевых кодовых слов.

Т.к. , то возникает вопрос о величине , такой, чтобы код обеспечивал контроль ошибок, т.е. обнаружение и исправление ошибок.

2 Контроль ошибок

Кодовое слово можно представить в виде вектора с координатами в – мерном векторном пространстве. Например, для вектор находится в трёхмерном евклидовом пространстве, рисунок 1.2. Разрешенными для передачи выбраны вектора и .

X₀

1 0 0 1 1 0

1 0 1 1 1 1

0 0 0 0 1 0 X₁

0 0 1 0 1 1

X₂

Рисунок 1.2

Рисунок дает наглядную алгебраическую интерпретацию понятия “мощность кода”:

а) кодовые слова полного кода определяют – мерное пространство, состоящее из последовательностей (– трехмерное пространство, состоящее при из 8 последовательностей полного кода);

б) кодовые слова избыточного кода определяют подпространство (подмножество) – мерного пространства, состоящее из последовательностей.

Под воздействием помех происходит искажение отдельных разрядов слова. В результате разрешённые для передачи кодовые векторы переходят в другие векторы (с иными координатами) – запрещённые. Факт перехода разрешённого слова в запрещённое для передачи слово можно использовать для контроля за ошибками.

Возможна ситуация, когда разрешённый вектор переходит в другой разрешённый кодовый вектор: . В этом случае ошибки не обнаруживаются, и контроль становится неэффективным.

Из рассмотренной модели можно сделать следующий важный вывод: для

того чтобы передаваемые векторы можно было бы отличать друг от друга при наличии помех, необходимо располагать эти векторы в – мерном пространстве

как можно дальше друг от друга. Из этой же – мерной модели следует геометрическая интерпретация расстояния Хэмминга: – это число рёбер, которые нужно пройти, чтобы перевести один вектор в другой, т.е. попасть из вершины одного вектора в вершину другого.

2.1 Обнаружение и исправление ошибок

Стратегия обнаружения заключается в следующем. Декодер обнаруживает ошибку при априорном условии, что переданным словом было ближайшее по расстоянию к принятому слову. Покажем применение этого утверждения.

Пример 1 . Пусть ; . Разрешенным для передачи является множество кодовых слов:

.

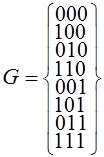Очевидно, что код имеет . Любая одиночная ошибка трансформирует данное кодовое слово в другое разрешенное слово. Это случай безизбыточного кода, не обладающего корректирующей возможностью.

Пример 2. Пусть теперь подмножество разрешённых кодовых слов предоставлено в виде двоичных комбинаций с чётным числом единиц.

.

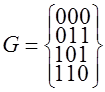Заданный код имеет . Запрещенные кодовые слова представлены в виде подмножества :

.

Если , то ни одно из разрешенных кодовых слов (т.е. кода ) при одиночной ошибке не переходит в другое разрешённое слово этого же кода. Таким образом, код обнаруживает:

– одиночные ошибки;

– ошибки нечетной кратности (для - тройные).

Например, тройная ошибка кодового слова ; , переводит его в запрещенный вектор .

Вывод – В общем случае, при необходимости обнаруживать ошибки кратности кодовое расстояние кода должно быть

.

Пример 3 . Пусть ; ; код задан векторами и .