Реферат: Расчет на прочность при напряжениях, циклически изменяющихся во времени
где nσи пτопределяются по формулам (12) и (13).
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЗАПАСА ПРОЧНОСТИ ПРИ НЕСИММЕТРИЧНОМ ЦИКЛЕ НАПРЯЖЕНИИ
Для расчетов при несимметричном цикле напряжений принимают упрощенную диаграмму CMLпредельных напряжений образца (рис. 12.6 и 12.14).
Учитывая концентрацию напряжений, влияние абсолютных размеров, состояние поверхности, строят диаграмму предельных напряжений детали. При этом в соответствии с данными опытов влияние перечисленных факторов
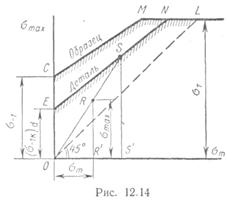
относят только к переменной составляющей цикла, т. е. к амплитуде σа. Предельная амплитуда I напряжений для образца, согласно формуле (7), равна
(14)
Предельная амплитуда напряжений для детали, согласно сказанному выше, равна
(15)
Уравнение линии предельных напряжений EN(см. рис. 12.14) \ для детали получит вид
(16)
Здесь штрихами обозначены текущие координаты.
Вычислим теперь коэффициент запаса прочности детали при действии переменных напряжений 
и 
(точка Rдиаграммы — см. рис. 12.14).
Предположим, что при увеличении нагрузки на деталь отношение 
. Такое нагружение называется простым. В этом случае предельной точкой, соответствующей разрушению, будет являться точка S.
Коэффициент запаса прочности будет равен отношению отрезков SS' к RR':
(17)
Величину 
(ординату точки S) найдем в результате совместного решения уравнений линии ENи линии OS. Уравнение линии OSимеет вид
(18)
Штрихами обозначены текущие координаты.
Приравняв правые части формул (16) и (18), получим
откуда
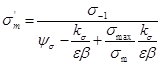
Подставив значение 
в формулу (16) или (18), найдем ординату точки S
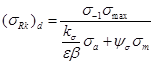(19)
Следовательно, на основании формулы (17) получается следующая окончательная зависимость для определения коэффициента запаса прочности
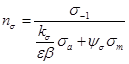(20)
Аналогично при кручении
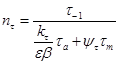(21)
При сложном напряженном состоянии, возникающем, например, при кручении с изгибом, коэффициент запаса прочности вычисляется по формуле (9.43)