Реферат: Расчет настроек автоматического регулятора
В программе Linreg задаем передаточную функцию объекта третьего порядка с запаздыванием. Выбираем ПИ-регулятор и определяем его настройки.
Получаем kp = 0.8743
Tu = 8.3924
В программе SIAM пользуясь схемой для одноконтурной системы получаем
- переходный процесс по заданию:
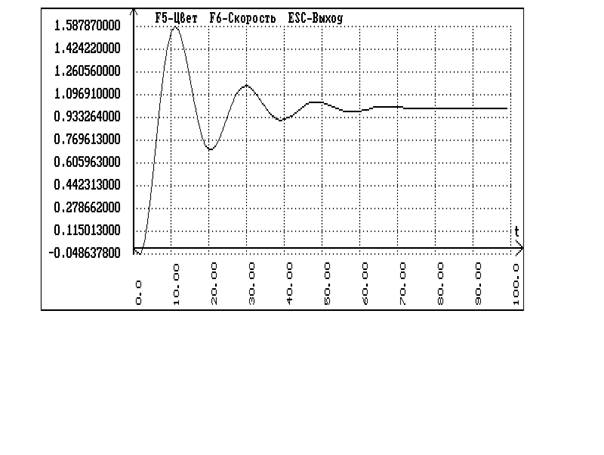
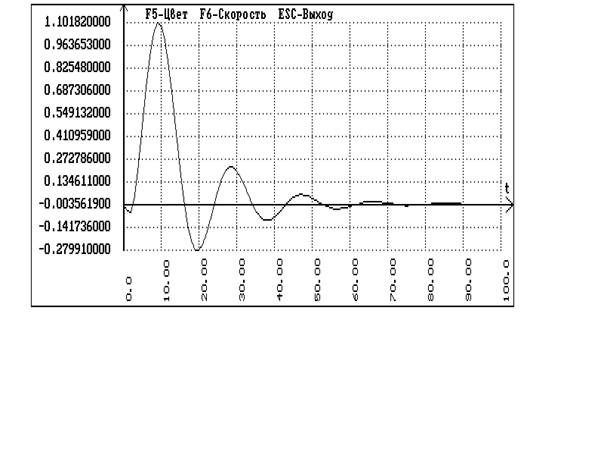
Расчет каскадной АСР методом Роточа.
а) для экспериментальной передаточной функции.
Первоначально определим настройки внутреннего регулятора для внутреннего контура с передаточной функцией W1(s).
0.4s + 1
W1(s) = --------------------------
2
14.0904s + 6.9614s +1
С помощью программы ASR получим АФХ по передаточной функции и определим значения u(m,w), v(m,w), a(m,w), w.
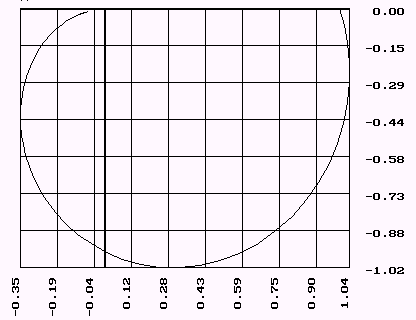
| v(m,w) | u(m,u) | a(m,w) | w | kp | Tu |
| 1,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
| 1,0211 | -0,0678 | 1,0234 | 0,0100 | 15,0783 | 0,0109 |
| 1,0360 | -0,1398 | 1,0454 | 0,0200 | 7,4774 | 0,0211 |
| 1,0439 | -0,2151 | 1,0659 | 0,0300 | 4,9709 | 0,0307 |
| 1,0442 | -0,2931 | 1,0845 | 0,0400 | 3,7336 | 0,0395 |
| 1,0361 | -0,3728 | 1,1012 | 0,0500 | 3,0067 | 0,0475 |
| 1,0194 | -0,4531 | 1,1156 | 0,0600 | 2,5367 | 0,0547 |
| 0,9936 | -0,5329 | 1,1275 | 0,0700 | 2,2147 | 0,0609 |
| 0,9587 | -0,6108 | 1,1368 | 0,0800 | 1,9877 | 0,0660 |
| 0,9147 | -0,6857 | 1,1431 | 0,0900 | 1,1826 | 0,0701 |
| 0,8619 | -0,7559 | 1,1464 | 0,1000 | 1,1713 | 4,4754 |
| 0,8008 | -0,8203 | 1,1464 | 0,1100 | 1,6386 | 4,5739 |
| 0,7323 | -0,8775 | 1,1429 | 0,1200 | 1,1584 | 0,0749 |
| 0,6576 | -0,9263 | 1,1360 | 0,1300 | 1,5905 | 0,0737 |
| 0,5778 | -0,9658 | 1,1254 | 0,1400 | 1,6169 | 0,0711 |
| 0,4945 | -0,9953 | 1,1114 | 0,1500 | 1,6842 | 0,0668 |
| 0,4095 | -1,0143 | 1,0938 | 0,1600 | 1,8064 | 0,0609 |
| 0,3243 | -1,0229 | 1,0731 | 0,1700 | 2,0137 | 0,0533 |
| 0,2407 | -1,0214 | 1,0493 | 0,1800 | 2,3750 | 0,0438 |
| 0,1601 | -1,0103 | 1,0229 | 0,1900 | 3,0885 | 0,0324 |
| 0,0840 | -0,9906 | 0,9942 | 0,2000 | 5,0095 | 0,0000 |
| 0,0134 | -0,9635 | 0,9635 | 0,2100 | 26,1125 | 0,0034 |
Так как настройки регулятора не могут быть отрицательными то ограничимся 3 квадрантом. И с помощью программы на BASIC рассчитаем оптимальные настройки для ПИ - регулятора методом Стефани по следующим формулам:
A^2(m,w) m 1
Tu = ------------------------ , kp = ---------- - ----------
w(m^2+1)* v(m,w) v(m,w) u(m,w)
наибольшее отношение kp/Tu и будет оптимальными настройками.
Получили что kp = 1.712763
Tu = 4.47537
В программе SIAM с помощью схемы для одноконтурной системы без запаздывания получаем переходные процессы по заданию и по возмущению:
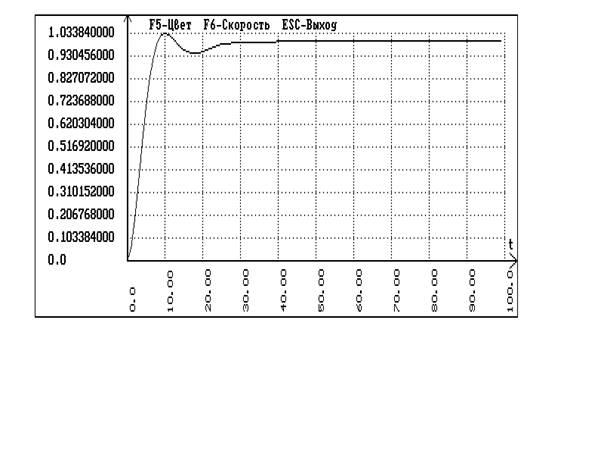
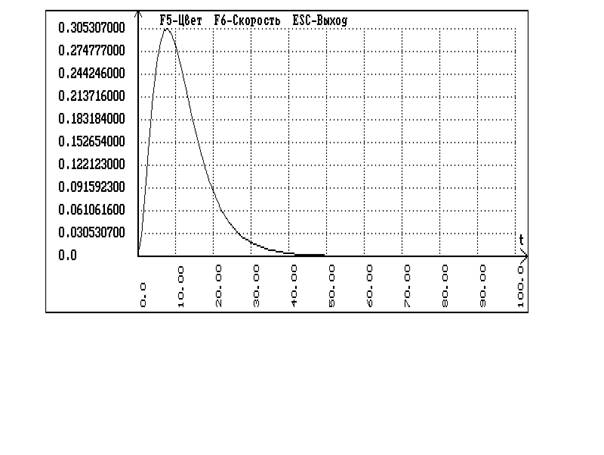
Сравнивая график кривой разгона по основному каналу и переходный процесс внутреннего контура каскадной системы делаем вывод о том, что за время запаздывания основного контура переходный процесс во внутреннем контуре затухнуть не успевает, следовательно передаточная функция эквивалентного объекта имеет вид:
Wоб(s) * Wp1(s)
Wоб(s) = --------------------------- =
1 + Wоб1(s) * Wp1(s)