Реферат: Расчет переходных процессов в линейных цепях с сосредоточенными параметрами

Задана электрическая цепь, изображенная на рисунке 1:

Требуется:

1) Определить выражения для всех токов в цепи в переходном режиме, решив задачу классическим и операторным методами.

2) Определить выражения для напряжений на емкости и индуктивности, решив задачу классическим и операторным методами.

3) Построить кривые напряжения токов во всех ветвях и напряжений на емкости и индуктивности в функции времени.

Заданные параметры цепи:

(Ом); (Ом);

(Гн); (мкФ)

1) Для t≥0 получим систему уравнений метода переменных состояния. Используя законы Кирхгофа, составим систему уравнений:

(1)	(2) (3) (4)

В качестве переменных состояния рассмотрим и , подставим уравнения (2,3,4) в систему (1), сведя ее к системе из двух уравнений:

(5)	Приведем систему уравнений (5) к нормальной форме.

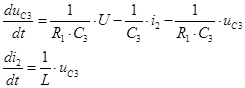(6)

2)

При определим принужденные составляющие. Учтем, что в установившемся режиме

(В/с); (А/с).

Тогда система (6) примет вид:

	(В)
			(А);

3)

Корни характеристического уравнения можно найти из выражения входного комплексного сопротивления схемы переменному синусоидальному току, т.е для t≥0

; заменяем на р и выражение приравниваем к нулю:

(1/с); (рад/с).

4)

С помощью законов коммутации находим начальные условия переходного процесса:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--