Реферат: Расчет переходных процессов в линейных цепях с сосредоточенными параметрами

(В).

Подставляя эти значения в систему (6) при t=0, получаем:

(В/с)

(А/с)

5)

Определим постоянные интегрирования, для этого составим систему уравнений. Первое уравнение системы – это уравнение искомой величины. Оно записывается в виде суммы принужденной и свободной составляющих. Принужденная составляющая найдена выше. Свободная составляющая записывается в соответствии с видом корней характеристического уравнения. При двух комплексных сопряженных корнях свободная составляющая представляет собой затухающую синусоиду, которая содержит две постоянных интегрирования А и . Для их определения необходимо второе уравнение. Его получают дифференцированием первого:

При t=0 система сведется к виду:

Решение системы дает: ; А= 37,79 (В);

Искомое решение для напряжения на емкости принимает вид: (В).

Аналогичным образом находим решение для тока второй ветви:

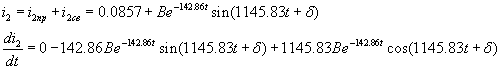
При t=0:

0.075= 0.0857+

50=

Искомое выражение для тока второй ветви:

(А);

Определение :

Согласно уравнению (3) , (В);

Из системы (1):

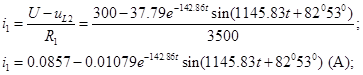
II. Операторный метод расчета

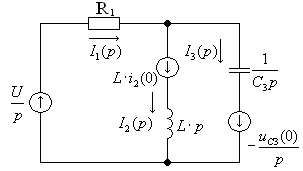
1) Составляется операторная схема замещения исходной электрической цепи (Рис.1) для времени . При этом все известные и неизвестные функции заменяются изображениями. Для нахождения параметров дополнительных источников операторной схемы замещения с помощью законов коммутации определяются независимые начальные условия (НУ):

(А); (В).

2) Находится изображение искомого тока. Операторная схема замещения содержит 3 источника в разных ветвях: основной и два дополнительных. Поэтому для нахождения изображения тока второй ветви воспользуемся законами Кирхгофа в операторной форме: