Реферат: Расчет размерных цепей
Задание.
Решить прямую задачу размерной цепи механизма толкателя, изображённого на рисунке 1.1., методами максимума-минимума и вероятностным. Способ решения стандартный,
А3 = 100 мм 
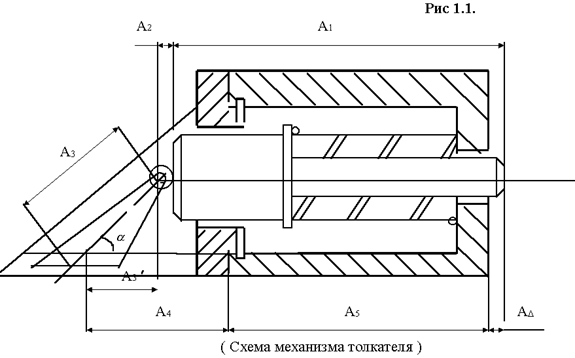
Обозначения:
А1 – длина поршня;
А2 – радиус поршня;
А3 – расстояние между осями отверстий в толкателе;
А4 – расстояние от торца крышки до оси отверстия в ней;
А5 – длина корпуса;
А
- вылет поршня за пределы корпуса;
Таблица 1.1. ( исходные данные )
| А1 , мм | А2 ,мм | А3 ,мм | А4 ,мм | А5 ,мм | А ,мм |  ,град | %,риска |
| 175 | 20 | 100 W | 110 W | 153 | А +0,45 | 420 | 1,0 |
Аi – номинальные размеры составляющих звеньев,
А - предельное отклонение размера
( ??3 = А3 Сos )
Краткая теория.
Основные определения.
Размерная цепь – совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи. Размерные цепи бывают плоские, параллельные и пространственные. Замкнутость – является обязательным условием размерной цепи.
Размерные цепи состоят из звеньев:
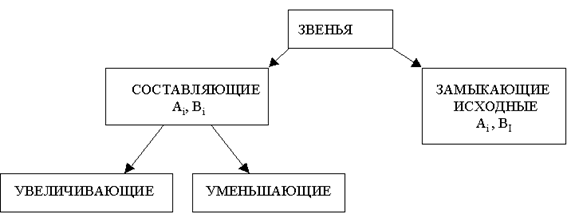
Замыкающий размер ( звено ) – размер ( звено ), которое получается при обработке деталей или при сборке узла последним.
Увеличивающий размер ( звено ) – размер ( звено ), при увеличении которого замыкающий размер увеличивается.
Для плоских параллельных размерных цепей 
= +1
Где: 
= 
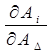- коэффициент влияния.
Уменьшающий размер – размер, при увеличении которого замыкающий размер уменьшается. = -1
Задачи размерных цепей.
Существует две задачи для размерных цепей: прямая и обратная.
Обратная задача заключается в определении номинального размера, координат середины поля допуска и предельных отклонений замыкающего звена при заданных аналогичных значениях составляющих звеньев.
( синтез ) заключается в заключении номинальных размеров, координат середин полей допусков, допусков и предельных отклонений составляющих звеньев по заданным аналогичным значениям исходного звена.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--