Реферат: Расчет технических характеристик систем передачи дискретных сообщений

* нарисовать структурную схему оптимального приемника и записать

алгоритм работы;

* вычислить вероятность неправильного приема декретного двоичного

сигнала при отношении энергии сигнала к спектральной плотности

шума на выходе детектора h² =169;

* построить графики зависимости P_ош =f(h) для ЧМ и ФМ и сравнить их.

Целью оптимального приема повышение верности принимаемого сообщения, эта задача решается выбором оптимальной структуры приемника.

Задача приемника заключается в следующем: он анализирует смесь сигнала и шума Z(t) в течение единичного интервала времени и на основании этого анализа принимает решение, какой из возможных сигналов присутствует на входе приемника. Структурная схема оптимального демодулятора, построенного на согласованных фильтрах для приёма ЧМ сигнала приведена на рис.6.

Е₁ /No

СФ1 АД1 СУ1

Z(t) РУ bi*

СФ2 АД2 СУ2

Е₂ /No

Рис.6

Смесь сигнала и шума Z(t) фильтруется согласованным фильтром, а затем выделяется огибающая сигнала на выходе этого фильтра. Огибающая сравнивается с пороговым уровнем, величина которого при равных априорных вероятностях P(U1(t)=P(U2(t) определяется соотношением Ei/No. Если эти вероятности не равны, пороговый уровень изменится на lnP(U1(t)/P(U2(t). При превышении порогового уровня в верхнем канале принимается решение bi*=1, а если в нижнем, то bi*=0. Временные диаграммы поясняющие работу оптимального демодулятора ЧМ сигнала приведены на рис.7

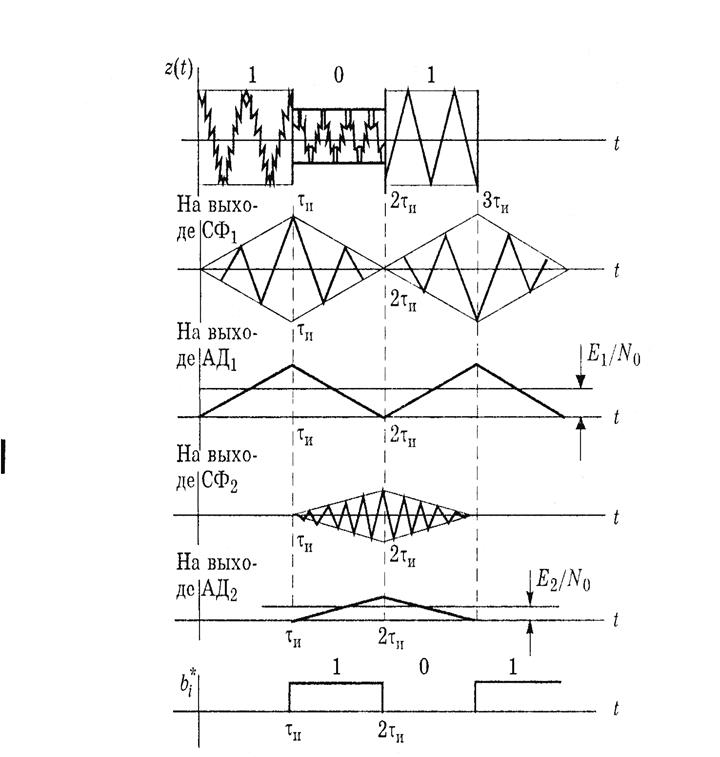
Рис. 7.

Алгоритм приёма имеет вид:

Т Т

ò Z(t)×Si(t)dt – 0.5Ei > ò Z(t)×Sj(t)dt – 0.5Ej; j¹i,

^{0 0}

где Ej – энергия ожидаемого сигнала.

Устройство, непосредственно вычисляющее скалярное произведе-

ние: Т

(Z,Si) – ò Z(t)×Si(t)dt , называют активным фильтром, или коррелятором.

⁰

Поэтому приёмник реализующий данный алгоритм называют корреляционным.

Вероятность неправильного приёма дискретного двоичного сигнала для ЧМ модуляции, при отношении энергии сигнала к спектральной плотности шума на выходе детектора h² =169, определим по формуле:

P=0,5 e ^{–0.5 h2} =0,5 e ^{- 84,5} = 10^-37

Вероятность ошибки для ЧМ сигнала определяется по формуле:

P_ош =0,5[1-Ф(h)],

где 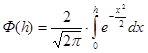- функция Крампа.