Реферат: Распределение Ландау
re – 2.818e-13 см – классический радиус электрона
M – молярная масса алюминия 27 г/моль
mc2 – энергия покоя электрона 0.511e6
с – скорость света 299792458 м/c
Проводиться розыгрыш равномерно распределенной случайной величины γ для определения длины пробега электрона.
Расчет длины пробега электрона:
L= – lnγ/ Σ(E)
Частицы регистрируются в заданной координате
Z*(Z*1 =Lmax/100, Z*2 =Lmax/10,
Lmax – максимальный пробег частицы). После чего частицы, дошедшие до данной точки, распределяются по потерям энергий с шагом в 1Кэв.
Заключение
В процессе работы алгоритм был реализован на языке программирования C++. По полученным данным были построены соответствующие графики для разных значений точки регистрации частиц, а также графики распределения Ландау. По графику распределения частиц по потерям энергии для расстояния Z*2 , можно утверждать, что полученные данные сходятся с теоретическими в определенных значениях. Для сравнения график распределения частиц по потерям энергии для расстояния Z*1 . Погрешности в данной работе носят систематический характер.
Список литературы
1. М.Е. Жуковский, М.В. Скачков. «Статистические модели электронной эмиссии. Модель «Утолщенных траекторий»». М.: Препринт, Институт прикладной математики РАН, 2007.
2. A.M. Кольчужкин, В.В. Учайкин. «Введение в теорию прохождения частиц через вещество». М.: Атомиздат 1978.
3. И.М. Соболь «Метод Монте-Карло». М.: Наука 1968.
4. Лекции Научно-исследовательского института ядерной физики им. Д.В. Скобельцына.
Приложение
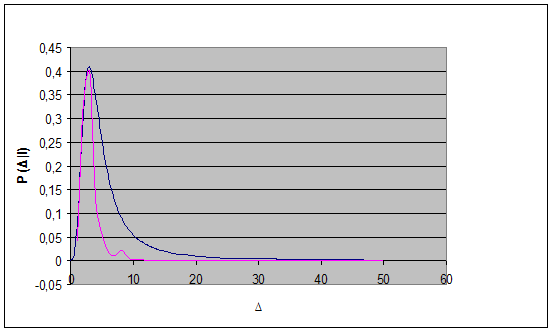
![]()
P (Δ|l) – распределение частиц по потерям энергии на пути l.
Δ – потери энергии, КэВ.