Реферат: Распределение Ландау

Введение

Математическое моделирование процессов взаимодействия ионизирующего излучения с объектами сложной геометрии и внутренней структуры имеет важное значение во многих приложениях. В частности, в рамках задач рентгеновской диагностики материалов и конструкций требуется определить и исследовать рентгеновские изображения объектов, а при изучении электромагнитного воздействия проникающего излучения необходимо проанализировать распределение потоков релятивистских электронов, возникающих в результате взаимодействия ионизирующего излучения с материалами объектов.

Математическое моделирование процессов трансформации проникающего излучения в материалах объектов проводилось в большом количестве научных работ. В одних работах используются и развиваются сеточные методы решения уравнения переноса излучения. В других разрабатываются вычислительные алгоритмы, основанные на статистическом моделировании методом Монте-Карло процессов переноса и взаимодействия излучения с веществом. Преимущество метода Монте-Карло перед альтернативными методами, основанными на численном решении кинетического уравнения, определяется удобством и приспособленностью этого метода к решению сложных граничных задач в многокомпонентных средах.

1. Основная часть

В данной работе будет рассматриваться взаимодействие электронов с веществом.

Прохождение пучка эл-в с энергией Е0 через образец сопровождается многообразными явлениями, часть из которых схематично изображена на рис. 1.1.

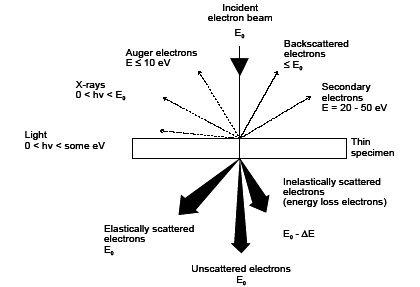
Рис. 1.1. Основные процессы при взаимодействии с веществом

Среди них – прежде всего рассеяние и дифракция электронов, генерация рентгеновского излучения, фотонов низкой энергии и другие процессы. Интенсивность процесса характеризуется сечением процесса, обозначаемым σ и имеющим размерность. Если образец имеет толщину t, плотность атомов N, плотность ρ, и атомный вес A, то интенсивность процесса, скажем, рассеяния, будет

QТt = NtσT = N0σТρt/A,

где N0 – число Авогадро. Значок T означает интенсивность полного или интегрального сечения, в отличие от дифференциального, описывающего угловое распределение,

dσ/dΩ = (1/(2πsinθ)) dσ/dθ.

Вместо сечения, имеющего размерность площади, часто используют среднюю длину пробега между последовательными актами взаимодействия (mean free path), приводящими к наблюдаемому процессу

Λ = 1/Q = A/(N0σρ).

В данной работе стоит задача о рассеянии электронов, поэтому рассмотрим данный процесс более подробно.

Для типичных толщин образцов (100 нм), большинство электронов проходят его не испытав рассеяния (unscattered electrons), либо испытав один акт столкновения (single scattering), кратное число (1<n<20) столкновений (plural scattering) или многократное (n>20) рассеяние (multiple scattering). Столкновения бывают упругими и неупругими.

Упругое рассеяние (elastically scattered electrons). Упругие столкновения – это такие, при которых энергия не расходуется на возбуждение атомов среды. Направление движения электрона может изменяться, но энергия практически не изменяется, т.е. Е ≈ Е0. Мы будем разделять упругое рассеяние на изолированном атоме и на системе атомов.

Упругое рассеяние на изолированном атоме. Проходя мимо атома на большом удалении от него, эл-н взаимодействует с эл-нами внешней оболочки и испытывает рассеяние на небольшой угол. Если же эл-н налетает на атом с малым прицельным параметром, то рассеяние может быть на большой угол, вплоть до 180º. С большой вероятностью электрон будет рассеян вперед, однако имеется малая вероятность рассеяния на большой угол (>90º). Упругое рассеяние на малые углы обычно вызвано рассеянием на электронах, а на большие углы – на ядрах.

Обратнорассеянные эл-ны имеют энергию, близкую к начальной и несут информацию о поверхности. Поскольку рассеяние никогда не является истинно упругим (как минимум, эл-н испускает тормозное излучение), то разделение на упругое и неупругое рассеяние является достаточно условным.

Сечение упругого рассеяния описывается формулой Резерфорда:

dσ(θ)/dΩ = e4Z2/[16E02sin4 (θ/2)]

Проинтегрировав по углу от 0 до π, для интегрального сечения будем иметь: σn = 1.62 10–24 (Z/E0) 2cot2 (θ/2).

Здесь сечение не учитывает электронную экранировку заряда ядра. Помимо этого, оно для нерелятивистских скоростей. Экранировку учитывают введением параметра Бора a0=4πħ2ε0/(m0e2)= 0.0529 нм, где ε0 – диэлектрическая константа, и введением поправки на экранирование.

Релятивизм эл-в учитывают введением соответствующей поправки для длины волны электрона

λ = 2πħ/{2m0E0 [1+E0/(2m0c2)]}1/2

В результате для дифференциального сечения получаем

dσ(θ)/dΩ=λ4 Z2/{64π4 (a0) 2 [sin2 (θ/2)+(θ0/2)2]2

Это т.н. экранированная релятивистская формула Резерфорда, хорошо работающая до энергий 300–400 кэВ и для Z<30. Важно помнить, что сечение рассеяния (σ, Q) эл-нов уменьшается с ростом энергии Е0.

Упругое рассеяние на системе атомов в отличие от классического корпускулярного подхода, описывается в рамках волнового механизма взаимодействия. Формула Резерфорда, даже с поправками на экранировку и релятивизм не могут точно описать процесс рассеяния, поскольку она игнорирует волновую природу электронов.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--