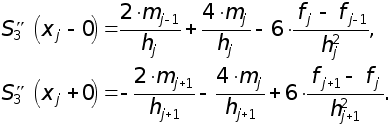Реферат: Разработка алгоритмов и диалоговых программ автоматизированного формирования

f₁ f_i f_N

f₀

x₀=a x₁ x₂ x_i x_N=b x

рис. 1.

Сплайном - называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a,b], а на каждом частичном отрезке [x_i, x_i+1] в отдельности является некоторым многочленом n-й степени :

, x_i i+1

Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, разность между степенью сплайна и порядком наивысшей непрерывной на [a,b] производной - дефектом сплайна. На практике наиболее широкое применение получили кубические сплайны S₃(x), имеющие на [a,b] непрерывную, по крайней мере, первую производную. Величина m_i = называется наклоном сплайна в точке (узле) x_i . Кубический сплайн S₃(x), принимающий в узлах x_i, x_i+1 соответственно значения f_i, f_i+1, имеет на частичном отрезке [x_i, x_i+1] следующее выражение [ 3 ] :

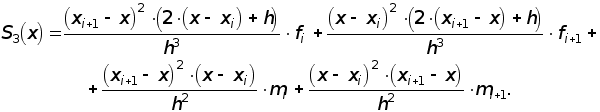(1.1)

Видно в (1) , что S₃(x_i)=f_i , S₃(x_i+1)=f_i+1 , а . Обозначим через значение в узле x_i справа, найденное непосредственно из выражения (1.1), а через - значение в узле x_i слева, т. е. найденное из соответствующего выражения S₃(x) на частичном отрезке [x_i-1, x_i], которое получается из (1.1) заменой i на i-1. Имеем

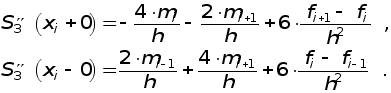
Требуем непрерывность в в узлах :

=, i= 1 , 2, ..., N-1,

и приходим к следующей системе линейных алгебраических уравнений относительно наклонов m_i :

, i= 1, 2, ..., N-1 (1.2)

и два краевых условия (они обычно связаны с “крайними” значениями m₀ и m_N). В программе использовались три варианта краевых условий :

1. Если известны , то задаем

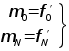(1.3)

2. Производные аппроксимируем формулами численного дифференцирования третьего порядка точности (применение интерполяционного полинома Лагранжа [ 3 ]) и, отбрасывая остаточные члены, полагаем :

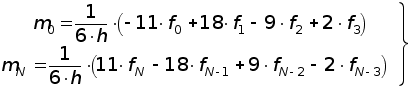(1.4)

3. В некоторых случаях бывают известны значения на концах отрезка [a,b], т. е. величины . Тогда требования приводят к краевым условиям :

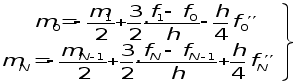(1.5)

Краевые условия (1.3) - (1.5) можно комбинировать, т. е. В левом и правом крайних узлах выбирать их независимо. Система (1.2) при всех рассмотренных краевых условиях имеет единственное решение [ 4 ], для нахождения которого могут быть применены методы прогонки и итераций. Решив систему (1.2) при выбранных краевых условиях, находим наклоны m_i, i= 0, 1,..., N, во всех узлах. Затем по формуле (1.1) задаем сплайн на каждом частичном отрезке [x_i-1, x_i], i= 0, 1, ...., N-1. Построенный данным способом сплайн S₃(x) имеет дефект не больше единицы, так как он обладает на отрезке [a,b] непрерывной второй производной .

Если рассмотреть кубический сплайн с переменными шагами, тогда на отрезке [x_j-1, x_j] он имеет следующее выражение [ 4 ] :

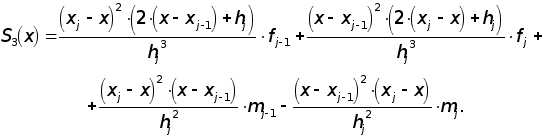(1.1.a)

взяв от которого две производные получим :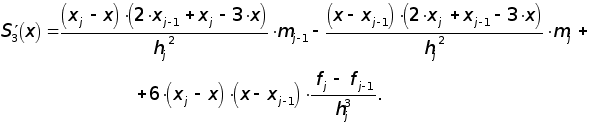

Отсюда находим

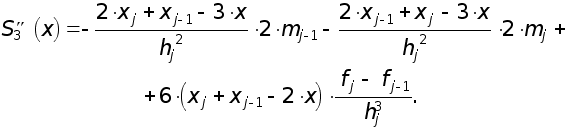
и