Диаграмма направленности симметричного вибратора может быть получена с помощью метода, имеющего большое значение в теории и технике антенн и применяющегося для получения диаграмм направленности любых антенн. Метод предполагает распределение комплексной амплитуды тока по антенне известным.

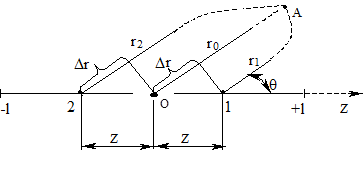
Рис.2.2. К выводу формулы поля симметричного вибратора.

В основе метода лежит принцип суперпозиции или наложения.

При выводе формулы диаграммы направленности антенна рассматривается как совокупность элементарных излучателей, поля от которых надлежит суммировать в текущей точке наблюдения, расположенной в дальней зоне на сферической поверхности радиуса r.

Разберём указанный метод и выведем формулу для диаграммы направленности симметричного вибратора.

На рис.2.2 показан тонкий вибратор с выделенными на нём двумя симметрично расположенными диполями длинной dZ с координатами центров ±Z . Там же указана система координат для отсчёта положения точки наблюдения А и координат диполей с током.

Поскольку точка наблюдения отнесена в дальнюю зону, то есть на достаточно большое расстояние r₀ >>2l , то все лучи, направленные в точку наблюдения от различных диполей, можно считать практически параллельными. Это значит, что r₀ , r₁ и r₂ связаны между собой соотношениями:

r₂ - D r =r₀ =r₁ + D r , (2.12)

где

Dr =|Z|cos q.

Запишем поле от двух выбранных диполей, считая их достаточно тонкими (диаметр провода значительно меньше длины волны):

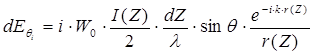, (2.13)

Сравнивая поля от двух противоположных элементарных вибраторов, видим, что они только отличаются значением множителя , то есть амплитудами, обратно пропорциональными расстояниями r(Z) , и фазами, прямо пропорциональными расстояниям:

Y =k × r(z) . (2.14)

При условии r>>l отличие амплитуд будет настолько несущественным, что с хорошей точностью модули полей от всех диполей можно определять через одно и то же расстояние r₀ , соответствующее середине симметричного вибратора.

Однако при оценке фазовых сдвигов полей с различием расстояний r₁ и r₂ нельзя не считаться.

С учётом принятых допущений поле от пары диполей записывается в виде:

, (2.15)

Чтобы получить значение полного поля и диаграммы направленности симметричного вибратора, необходимо просуммировать dE _q от всех пар симметрично расположенных диполей, составляющих оба провода антенны.

Сложение бесконечного числа элементарных полей осуществляется путём интегрирования выражения (2.15) в пределах одного плеча вибратора. Результирующее поле оказывается равным:

. (2.16)

В полученной формуле в квадратных скобках выделено произведение двух множителей, зависящих от q и представляет собой диаграмму направленности в меридиональной плоскости F( q). Каждому из множителей может быть приписан определённый физический смысл.

Ниже приведены графики для F( q) при различных отношениях .

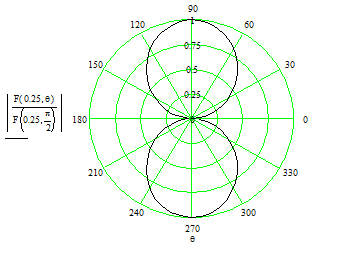
Рис. 2.3. Диаграмма направленности при l/l=0,25.

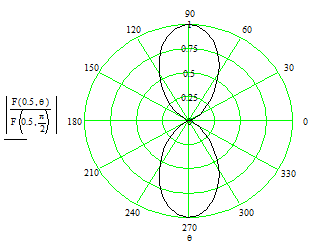
Рис. 2.4. Диаграмма направленности при l/l=0,5

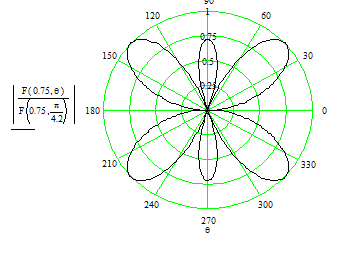
Рис. 2.5. Диаграмма направленности при l/l=
0,75

2.4.Схема замещения нелинейного резистора

Нелинейный резистор - элемент электрической цепи, напряжение и ток в котором связаны нелинейным законом. Для моделирования нелинейных резисторов в радиотехнике используются несколько методов, например, замена его на эквивалентный источник напряжения (тока), управляемого током (напряжением).

В нашем случае в качестве нелинейного резистора используется диод. Для моделирования диода будем использовать зависимость тока диода от напряжения i =f (U), приложенного к его концам, то есть, заменяем источником тока, управляемым напряжением. Эту зависимость запишем аналитически в виде i =I₀ ×e^aU , которая хорошо согласуется с экспериментальными данными. Кроме того, диод обладает паразитной индуктивностью выводов и паразитной ёмкостью корпуса. Паразитная ёмкость корпуса моделируется включением ёмкости соответствующего номинала параллельно источнику тока, а паразитная индуктивность включением эквивалентной индуктивности последовательно с ним.

2.5.Схема замещения нелинейной ёмкости

Нелинейная ёмкость – элемент, ёмкость которого зависит от приложенного напряжения. В качестве нелинейной ёмкости берётся варикап. Поскольку варикап является диодом и включается в обратном смещении то считается, что его активное сопротивление равно бесконечности. Как и диод варикап обладает паразитной ёмкостью корпуса и паразитной индуктивностью выводов, которые моделируются аналогично паразитной ёмкости и индуктивности диода.

Получаем в качестве модели варикапа ёмкость, управляемую напряжением, с параллельно и последовательно включёнными паразитной ёмкостью и индуктивностью. Зависимость ёмкости от напряжения выражается следующей функцией:

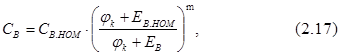
где С_В.НОМ – ёмкость варикапа, приведённая в справочнике при напряжении смещения Е_В.НОМ ;

j_к – контактная разность потенциалов для кремниевого варикапа равна 0,65.

m – коэффициент степени (для сплавных m=0.5, для диффузионных m=0.3)

3. СОСТАВЛЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОТРАЖАТЕЛЯ – МОДУЛЯТОРА

Математическая модель отражателя - модулятора необходима для моделирования этого устройства с помощью вычислительной техники. Предполагается, что все элементы математической модели будут представлены как совокупность элементарных пассивных элементов с постоянными или переменными параметрами. Эта модель позволит анализировать параметры отражателя – модулятора с помощью специальных программных продуктов, предназначенных для расчёта электрических цепей и схем.

Основной задачей моделирования является создание схемного аналога вибратора – антенны отражателя - модулятора, поскольку этот элемент устройства имеет большой разброс параметров для различных частот, а нам необходима общая модель для всего рабочего диапазона частот, который имеет коэффициент перекрытия три и более. Поэтому, разработке модели именно вибратора в данном разделе будет уделено особое внимание, поскольку задача является далеко не тривиальной, кроме того аналогичной задачи не рассматривалось ни в одной книге, просмотреной в ходе подготовке к дипломной работе. Разработанный мною метод моделирования может с успехом применяться для моделирования и других цепей, поскольку в ходе моделирования был использован общий подход.