Реферат: Реализация программы Кредитный калькулятор и оценка ее эффективности

Существуют различные определения эффективной процентной ставки. В случае автокредитования, наилучшим определением является такое: эффективная процентная ставка – это годовая ставка сложных процентов, без начислений в году и дающая тот же финансовый результат, что и любая другая ставка (рассчитывается с учетом всех расходов, произведенных за время пользования кредитом). Следует отметить, что поскольку при расчете эффективной процентной ставки учитываются все сборы и комиссии банков, то очень большое значение имеет время кредита.

В автомобильном кредите существует такой термин как удорожание автомобиля. Удорожание автомобиля, это процентная разница между суммой, которая будет потрачена на покупку автомобиля в кредит, и суммой начальной стоимости автомобиля. Процент удорожания автомобиля удобен для сравнивания предложений нескольких банков, но совершенно не подходит как показатель выгодности кредита. Не стоит забывать о том, что за срок выплаты кредита ценность денег неизменно упадет из-за инфляции. Можно сказать, что при нормальных условиях кредит будет даже выгоднее, потому что итоговые затраты к концу периода будут меньше, чем затраты на обычную покупку автомобиля.

Ежемесячный платеж заемщика состоит из двух частей. Это – деньги, направляемые на возврат долга и проценты за пользование кредитом. Каждый месяц заемщик возвращает часть своего долга. После того, как заемщик вернул часть денег, на возвращенную заемщиком часть денег проценты больше не начисляются. Проценты за пользование кредитом начисляются на остаток ссудной задолженности заемщика.

Рассмотрим два способа погашения кредитной задолженности.

2.1 Математическая модель аннуитетныхплатежей

В большинстве банков принято, что бы заемщик возвращал долг ежемесячно равными долями. Эффективность данного метода очевидна, банк легко может определить платежеспособность заемщика, взяв 40% от его ежемесячного дохода и сравнив с ежемесячной уплатой долга. Простой, на первый взгляд, метод подразумевает под собой сложные математические вычисления.

Рис. 1 Модель погашения кредита

Рис. 1 иллюстрирует схему погашения кредита равными долями за равные промежутки времени. Угол A отражает процентную ставку за период, на которые поделен срок кредита. AC - это сумма кредита . Y1 , Y2 , Y3 и так далее - это проценты, соответственно, за первый, второй, третий и так далее период. X1 , X2 , X3 и так далее - это часть основного долга, выплачиваемая вместе с процентами за, соответственно, первый, второй, третий и так далее период.Пусть S - сумма, взятая в долг, Q - годовая процентная ставка. Если принять месячную процентную ставку за x, тогда проценты за первый месяц пользования кредитом составят Sx, а долг составит

или, если обозначить число (1+x) через q,

Если не отдать проценты за первый месяц, то они прибавятся к основному долгу, и проценты за второй месяц будут начисляться на всю сумму. Проценты за второй месяц составят . Долг за два месяца составит

Если не отдать проценты и за второй месяц, то они также прибавятся к основному долгу, и проценты за третий месяц будут начисляться на всю сумму. Проценты за третий месяц составят . Долг за три месяца составит

Таким образом, долг за 12 месяцев, то есть за год, составит . В то же время, долг за год составляет . То есть получается следующее:

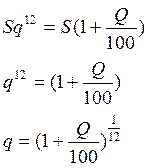
Теперь надо рассчитать размер ежемесячного (разового) платежа V. Чтобы с каждой выплатой долг уменьшался, размер разового платежа должен превышать сумму набежавших за месяц процентов, то есть разовый платёж состоит из двух частей: процентов за пользование деньгами Y и части основного долга X. То есть платёж за k-й месяц можно обозначить как , а платёж за следующий, то есть (k+1)-й, месяц - как . А поскольку платежи за все месяцы должны быть одинаковы, то:

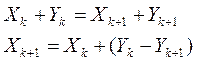
Разницу в процентах между двумя следующими друг за другом месяцами можно вычислить как длину катета в прямоугольном треугольнике, в котором известны тангенс противолежащего угла (q-1) и длина другого катета , то есть как произведение другого катета на тангенс прилежащего к нему угла:

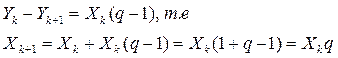
Тогда, если выплату из основного долга за первый месяц обозначить X1, выплата из основного долга за второй месяц составит:

выплата из основного долга за третий месяц:

выплата из основного долга за n-й месяц:

Таким образом сумму кредита (S) можно записать так:

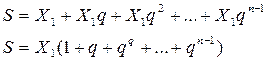
Отсюда:

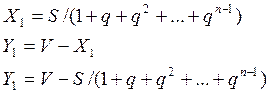
А поскольку основной долг за первый месяц - это S, то проценты за первый месяц составят , тогда:

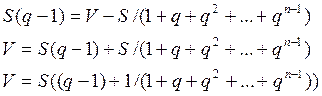
- это сумма первых членов геометрической прогрессии со знаменателем , поэтому, используя формулу суммы первых членов геометрической прогрессии:

можно переписать полученную формулу так:

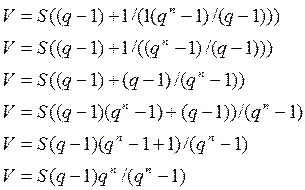
Итак, можно найти ежемесячный равнодолевой платеж клиента, зная сумму кредита, процентную ставку и срок выплаты кредита используя формулы:

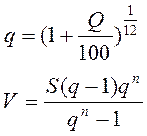
Где:

- V – ежемесячный равнодолевой платеж клиента

- S – сумма кредита (если нет первого взноса, то цена автомобиля)

- Q – процентная ставка кредита

- n – количество ежемесячных выплат.

Напомним, что в автокредитовании есть понятие первого взноса, то есть частичная оплата стоимости автомобиля. Чем больше первый взнос, тем меньше сумма кредита и, соответственно, риска. Но в договоре кредитования стоит обращать внимание на строчки, содержащие слова «… от стоимости автомобиля». В этом случае банк говорит о сумме стоимости автомобиля, что значительно выше, чем сумма кредита.

Не стоит забывать, что помимо обычной процентной ставки существует добавочный процент, начисляемый за работу комиссии, страхования, страховании залога и так далее. Схема начисления добавочного процента должна оговариваться теми, кто ее взимает. Например, процент за обслуживание счета комиссией берется от той суммы, которую клиент выплачивает каждый месяц. Если процент ежемесячного начисления к оплачиваемой сумме обозначить как p , то итоговая сумма равна: