Реферат: Релаксорные сегнетоэлектрики в системе твердых растворов

Если же формирование эластомера происходит в монодоменном нематическом состоянии, а переход его в изотропное состояние с реализуется путем нагревания, то имеет место сокращение эластомера, характеризуемое величиной

. (5)

Зависящие от частоты вязко-упругие свойства среды определяются временными корреляционными функциями микроскопического тензора напряжений. Упомянутый тензор выражается через тензор ориентационного параметра порядка следующим образом:

, (6)

где характеризует степень удлиненности жесткого фрагмента молекулы, p – отношение длины фрагмента к его диаметру, – компоненты директора, b – величина, определяющая интенсивность взаимодействия в используемом потенциале среднего поля.

Временная корреляционная функция микроскопического тензора напряжений имеет вид

, (7)

где V – объем системы, – тензор релаксации напряжений.

Так как микроскопический тензор напряжений определяется через тензор , то вычисление функции сводится к вычислению временной корреляционной функции величины .

С учетом одноосной симметрии нематического эластомера тензор релаксации напряжений определяется следующим выражением

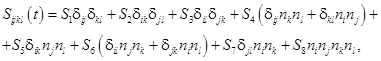(8)

где () – являются некоторыми неизвестными функциями времени t.

Введем нормированную функцию напряжений . При вычислении этих функций применим метод функций памяти Цванцига-Мори.

Комплексная корреляционная функция может быть представлена в виде

,, , . (9)

Тогда, зависящие от частоты коэффициенты вязкости определяется как

. (10)

Для вычисления функции использовано уравнение Цванцига-Мори

, (11)

где – функция памяти, которую будем моделировать с помощью функции

(12)

Параметры и выражены через коэффициенты разложения в ряд по времени функции релаксации напряжений вплоть до . Величина определяется формулой

, (13)

в которой , .

В итоге коэффициенты вязкости определяются как

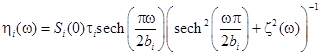, (14)

в которой (i = 1–8) имеют смысл некоторых времен корреляции, а выражается через функцию памяти (12).

Численные результаты для времен корреляции и коэффициентов вязкости при нулевых частотах получены при K, м–3 (число фрагментов в единице объема): с, с, с, с, с. В свою очередь коэффициенты вязкости при равны: Пас, Пас, Пас, Пас, Пас, Пас.

Полученные впервые численные результаты имеют разумный физический смысл для невырожденных состояний нематических эластомеров. В невырожденном случае коэффициенты вязкости , , , при ведут себя как .