Реферат: Решение иррациональных уравнений

При решении уравнений, содержащих радикалы 3-й степени, бывает полезно пользоваться сложением тождествами:

Пример 1.

.

Возведём обе части этого уравнения в 3-ю степень и воспользуемся выше приведённым тождеством:

Заметим, что выражение стоящее в скобках равно 1, что следует из первоначального уравнения. Учитывая это и приводя подобные члены, получим:

Раскроем скобки, приведём подобные члены и решим квадратное уравнение. Его корни и . Если считать (по определению), что корень нечётной степени можно извлекать и из отрицательных чисел, то оба полученных числа являются решениями исходного уравнения.

Ответ: .

Решение 2

Возведём две новые переменные и , тогда ,

.

Заметим, что .

В итоге получим систему уравнений:

Используя первоначальные уравнения системы, преобразуем вторые, заменив первую скобку единицей, а вторую подставим вместо неизвестного у выражение , также полученное из первого .

Приведём подобные члены, раскрыв предварительно скобки и решив полученное квадратное уравнение. Его корни и . Вернёмся теперь к начальной подстановке и получим искомые решения:

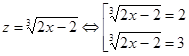
Введение нового неизвестного.

Решив эти уравнения, найдём радикалы более высоких степеней, но наиболее часто использовавшийся способ их решения – введение нового(новых) неизвестного.

Пример 2.

Обозначим , тогда

а)

Уравнение примет вид:

Корень не удовлетворяет условию

Ответ: 76.

Методы решения иррациональных уравнений.