Реферат: Решение нелинейных уравнений с одной переменной
Пусть уравнение F(x)=0 имеет единственный корень на отрезке [a, b]. Если отрезок [a, b] достаточно мал, то можно считать, что функция y=F(x) монотонна на этом отрезке и не меняет направление выпуклости. Значит на отрезке [a, b] нет точек максимума и минимума, т.е. ![]() . Т.к. направление выпуклости не меняется то и
. Т.к. направление выпуклости не меняется то и ![]() . Получаем четыре вида графиков, которые объединяются в два типа.
. Получаем четыре вида графиков, которые объединяются в два типа.
|
I. тип. Условие:
|
II. тип. Условие:
|
Пусть x* - искомый корень уравнения F(x)=0. Заменим кривую графика на хорду АВ. Уравнение прямой, проходящей через точки А (а, F(а)) и В(b, F(b)) имеет вид: ![]() , где (x, y) – любая точка прямой АВ. В качестве этой точки возмем точку пересечения хорды с осью ОХ, т.е.
, где (x, y) – любая точка прямой АВ. В качестве этой точки возмем точку пересечения хорды с осью ОХ, т.е.
|
(x1 , 0). Получим ![]() или .
или .
 Рассмотрим случай, когда кривая графика функции y= F( x) относится к I типу. Через точки А1 и В проводим следующую хорду. Она пересекает ось ОХ в точке х2. Аналогично получаем
Рассмотрим случай, когда кривая графика функции y= F( x) относится к I типу. Через точки А1 и В проводим следующую хорду. Она пересекает ось ОХ в точке х2. Аналогично получаем
![]() ,
,
…………………………………
| |
![]() (1)
(1)
Полученная таким образом формула (1) называется формулой метода хорд для кривых I-го типа.
Очевидно, что последовательность значений х1 , х2 , х3 , …,хn стремится к корню уравнения х* , а значит этот корень можно найти с заданной точностью.
|
(2)
Если на n-ом шаге![]() , то считается, что необходимая точность е достигнута.
, то считается, что необходимая точность е достигнута.
1.6. Уточнение корней методом касательных
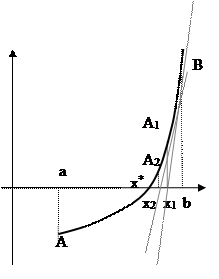 При уточнении корней методом касательных все функции делятся на два типа, как и в методе хорд. Рассмотрим кривую I-го типа.
При уточнении корней методом касательных все функции делятся на два типа, как и в методе хорд. Рассмотрим кривую I-го типа.
Проведем касательную к графику функции в точке В. Она пересечет ось ОХ в точке х1. Через эту точку проведем прямую перпендикулярную оси ОХ до пересечения с графиком функции. Получим точку А1 . Через неё опять проведем касательную. Получим точку х2 . Продолжая этот процесс, получим последовательность х1 , х2 , х3 , …,хn, сходящуюся к х* .
|
|
|
Если на n-ом шаге![]() , то считается, что необходимая точность е достигнута.
, то считается, что необходимая точность е достигнута.
1.7. Уточнение корней комбинированным методом хорд и касательных
Методы хорд и касательных дают приближение корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом. В этом случае процесс уточнения корня идет быстрее.
Метод реализуется по следующей схеме:


