Реферат: Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 10 Линейная алгебра (разное)

т.е.

Задача 7. Найти матрицу линейного оператора в базисе, где , если она задана в базисе .

, .

Найдем .

, .

Значит матрица в базисе имеет вид .

Задача 8. Доказать линейность, найти матрицу (в базисе ), образ и ядро оператора поворота относительно оси в положительном направлении на угол .

Если то .

Оператор является линейным, если

и .

.

.

Т.е. оператор А является линейным и его матрица .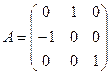

Область значений оператора А — это множество всех векторов .

Ядро линейного оператора — множество векторов, которые А отображает в нуль-вектор:

.

Задача 9 . Найти собственные значения и собственные векторы матрицы.

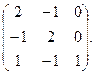
Составляет характеристическое уравнение и находим его решение.

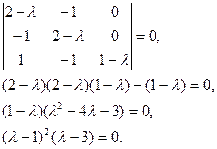
Собственные значения:

Найдем собственные вектора.

, ;

, .

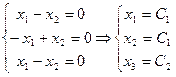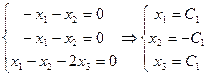Собственные вектора: