Реферат: Себестоимость прироста КРС
Остальные встречающиеся на практике показатели себестоимости можно подразделить по следующим признакам:
- по составу учитываемых расходов - цеховая, производственная, полная себестоимость;
- по длительности расчетного периода - месячная, квартальная, годовая, за ряд лет;
- по характеру данных, отражающих расчетный период, - фактическая (отчетная), плановая, нормативная, проектная (сметная), прогнозируемая;
- по масштабам охватываемого объекта - цех, предприятие, группа предприятий, отрасль, промышленность и т.п.
2 ЭКОНОМИКО-СТАТИСТИЧЕСКИЙ АНАЛИЗ СЕБЕСТОИМОСТИ ПРИРОСТА КРС
2.1 Группировка хозяйств по себестоимости прироста КРС
Важнейшим методом статистики является метод группировок. Группировкой называется распределение изучаемых общественных явлений на однородные в качественном отношении группы по ряду существенных признаков.
Метод группировки обобщает данные по качественно однородным группам, представляет их в компактном, обозримом виде. Группировка создает основу для применения других методов статистического анализа.
Выдающийся русский ученый Д. П. Журавский дал определение статистике как науке категорического вычисления, т. е. науке о счете по категориям, группам. В этом определении подчеркивается одна из специфических черт статистической методологии. Необходимость применения группировки объективна и обусловлена, прежде всего, наличием качественных различий между изучаемыми явлениями. С помощью метода группировок решаются сложные задачи статистического анализа.
Соответственно различают три вида группировок:
1) типологические группировки, с помощью которых выделяются социально-экономические типы общественных явлений. Примерами типологических группировок могут служить группировки хозяйственных объектов по формам собственности, населения — по общественным группам и социальному составу.
2) структурные, с помощью которых можно охарактеризовать состав, структуру совокупности по какому-либо признаку. Например, группировка населения по уровню образования, национальности, месту проживания. Деление группировок на типологические и структурные достаточно условно, например структурная группировка, проведенная по уровню среднего дохода на душу населения, может считаться и типологической;
З) аналитические группировки, которые проводят для того, чтобы установить взаимосвязь между явлениями и показателями. Явления, между которыми выявляется связь, называются явлением-фактором и явлением-результатом. Аналитическую группировку выполняют по признаку-фактору.
Явление-фактор — это явление, влияющее на величину другого явления, а явление-результат — это явление, которое зависит от другого явления, изменяется под его влиянием. Статистические группировки строятся как по одному, так и по нескольким признакам. Группировка по одному признаку называется простой, по двум или нескольким — комбинированной.
Построим ранжированный ряд по уровню себестоимости 1 ц. прироста КРС.
Таблица 2.1.1 Ранжированный ряд себестоимости1ц. прироста КРС
| № | Номер по порядку | Наименование хозяйств | Себестоимость 1 ц прироста КРС, руб. |
| 1 | 6 | ООО Агрофирма "Стерлитамакская" | 3802,07 |
| 2 | 3 | ООО "Агрофирма Аллагуват" | 4100 |
| 3 | 1 | СПК"Дружба" | 4993 |
| 4 | 5 | СПК им.Явнова | 5486,35 |
| 5 | 7 | Заря | 5622,2 |
| 6 | 2 | ГУСП"Стерлитамакское" РБ | 7317,77 |
| 7 | 4 | ГУСП совхоз "Рощинский" РБ | 7946,08 |
Изобразим ранжированный ряд графически
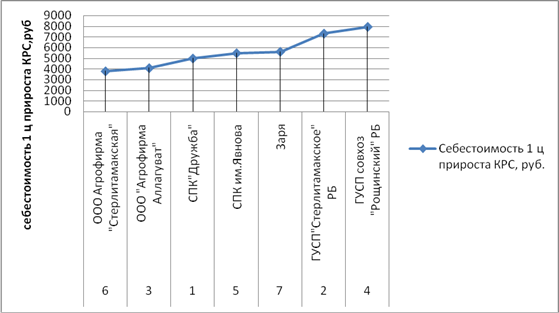
Рис.2.1.1 Ранжированный ряд себестоимости 1 ц прироста КРС
График показывает, что возрастание себестоимости идет постепенно.
Возрастание себестоимости от хозяйства к хозяйству происходит в основном плавно, с небольшими скачками. Поскольку между хозяйствами различия достаточно небольшие, то выделить типические группы на основе анализа ранжированного ряда в данном случае затруднительно. Поэтому далее необходимо построить интервальный ряд распределения хозяйств, оценить качественное состояние каждой группы путем построения промежуточной аналитической группировки и перейти от нее к типическим группам хозяйств.
i=(Xmax – Xmin)/n1 ,
i=(7946,08-3802,07)/2=2072,005
Распределим хозяйства по установленным группам и подсчитаем их число в группах таблица 2.1.2
Таблица 2.1.2 Интервальный ряд распределения хозяйств по себестоимости 1 ц прироста КРС
| № п/п | группы хозяйств по себестоимости 1 ц прироста КРС | число хозяйств |
| 1 | 3802,07-5874,07 | 5 |
| 2 | 5874,07-7946,08 | 2 |
| Итого | 7 |
Представим полученный интервальный ряд на диаграмме, в которой по оси абсцисс откладывается границы интервалов, а по оси ординат – численность группы.
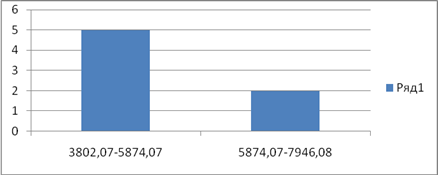
Рисунок 2.1.2 Интервальный ряд распределения хозяйств по себестоимости прироста КРС
Изучим характер вариации среднегодового поголовья КРС, определив показатели вариации для полученных групп.
По значению показателей асимметрии и эксцесса распределения можно судить о близости распределения к нормальному, что бывает существенно важно для оценки результатов корреляционного и регрессионного анализа, возможностей вероятностной оценки прогнозов. Распределение можно считать нормальным, т.к. показатели асимметрии и эксцесса превышают своих двукратных среднеквадратических отклонений.
Таблица 2.1.3 Исходные данные для расчета показателей вариации и формы распределения.
| Наименование предприятия | Себестоимость 1 ц прирост | Прирост крс, ц | x - x ̄ | (x - x̄)² | (x - x)²*f | ( x - x̄)*f | (x - x̄̄)3 | (x - x̄̄)4 | x*f |
| СПК"Дружба" | 4,99 | 2525 | 1,8 | 3,24 | 8181,00 | 4545,00 | 5,83 | 10,50 | 12607 |
| ГУСП"Стерлитамакское" РБ | 7,32 | 21184 | 0,5 | 0,25 | 5296,00 | 10592 | 0,13 | 0,06 | 155020 |
| ООО "Агрофирма Аллагуват" | 4,10 | 350 | 2,7 | 7,29 | 2551,50 | 945,00 | 19,68 | 53,14 | 1435 |
| ГУСП совхоз "Рощинский" РБ | 7,95 | 7752 | 1,1 | 1,27 | 9834,18 | 8731,24 | 1,43 | 1,61 | 61598 |
| СПК им.Явнова | 5,49 | 2858 | 1,3 | 1,69 | 4830,02 | 3715,40 | 2,20 | 2,86 | 15680 |
| ООО Агрофирма "Стерлитамакская" | 3,80 | 2875 | 3,0 | 9,00 | 25875,00 | 8625,00 | 27,00 | 81,00 | 10931 |
| Заря | 5,62 | 1027 | 1,2 | 1,44 | 1478,88 | 1232,40 | 1,73 | 2,07 | 5774 |
| Итого | 39,27 | 38571 | 11,6 | 24,18 | 58046,58 | 38386,04 | 57,99 | 151,24 | 263045 |
Чтобы рассчитать показатели асимметрии и эксцесса рассчитаем показатели:
Для начала найдем xср:
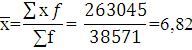
Рассчитаем показатели вариации:
Размах вариации – это разность между максимальным и минимальным значением варьирующего признака. Эта величина показывает, в каком пределе колеблется размер признака, образующего ряд распределения.
![]()
Среднелинейное отклонение – средняя из абсолютных значений отклонений отдельных вариант от их средней.
![]()
Дисперсия – среднеквадратическое отклонение значений признака от их средних величин.
![]()
Среднеквадратическое отклонение показывает, насколько в среднем отличается фактическое значение знака от своей средней величины.
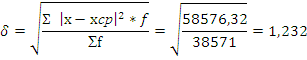
Относительные показатели вариации:
Коэффициент вариации:
![]()
Коэффициент осцилляции:
![]()