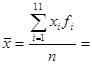Реферат: Середні Значення

Середні значення

Статистика оперує такими середніми значеннями: серед­нє арифметичне, середнє квадрати­чне, середнє геометричне.

Середнє арифметичне. Нехай ми маємо п об'єктів, у якихвиміряно деяку характеристику, що має значення x₁ ,x₂ , …, x_n .

Середнім значенням (або середнім арифметичним) називається таке число , яке дістають ді­ленням суми всіх да­них вибірки x₁ , _x2 , …, x_n на число цих даних n,

або (- знак суми – “сигма” велика)

Приклади. 1) Протягом перших п’яти днів березнятемпература повітря, вимірювана о 8 год. ранку, станови­ла 3°, 5°, 4°, 1°, 2°. Знайти середню температуру за ці дні.

Маємо:

2) 3 двох учнів треба вибрати одного в баскетбольну команду. Відомі кількості їхніх влу­чень м'яча в корзину накожні десять кидків під час тренувань.

Таблиця 1

Номер тренувань	1	2	3	4	5
Перший учень
4	3	5	3	6
Кількість влучень	Другий учень
5	4	3	6	5

Розв'язання.

Знаходимо середню кількість влу­чень.

Для першого учня:

Для другого учня:

Отже, в команду слід узяти другого учня.

Розглянемо деякі властивості середнього арифметичного.

1) Знайдемо відхилення l кожного значення x_j від се­реднього. Різниця х — може бути від'є­мною або додатною.

Сума всіх п відхилень дорівнює нулю. Проілюструє­мо цю властивість на при­кладі. Вихі­дні дані:. (0; 0; 1; 1; 3;3;3; 5); n= 8; = 2.

2) Якщо до кожного ре­зультату спостережень додати деяке число с (константу), то середнє арифметичне пере­твориться в + с. Візьмемо, наприклад, попередні 8 зна­чень і додамо до кож­ного з них по 5. Дістанемо числа 5; 5; 6: 6; 8; 8; 8; 10, середнє арифметичне яких (5 + 5+ 6 + 6 + 8 + 8 + 8+10) : 8 = 7. Середнє на 5 одиниць більше.

Таблиця 2

Значення	Середнє арифметичне	Відхилення
0	2	-2
0	2	-2
1	2	-1
1	2	-1
3	2	1
3	2	1
3	2	1
5	2	3
-
0

3) Якщо кожне значення сукупності з середнім по­множити на константу с, то середнє ариф­метичне стане с . Перевірте властивість, використовуючи попередні дані.

Якщо величини деяких даних повторюються, то середнє арифметичне визначають за фор­мулою

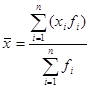,де

f_i — частота повторення результату x_i .

Приклади. 1) Протягом двадцяти днів серпня тем­пература повітря вранці була такою: 17°, 18°, 19°, 20°, 18°, 18°, 18^o , 19^o , 19°, 20°, 20°, 19°, !9°_, 19°, 20°, 19^o , 18°, 17°, 16°, 19°.

Знайти середню температуру за цими даними.

Тут окремі значення (17°, 18°, 19°, 20°) повторюються. Середня температура дорівнює:

2) Подаємо запис обчислення середнього арифметичного при повторенні деяких даних у ви­гляді таблиці.

Таблиця 3

Вихідні дані			xi	Час­тота fi	xi fi	Остаточне обчис­лення
2	6	10	2	2	4	де I=1,2,3,…,11
2	6	10	3	1	3
3	6	11	4	3	12
4	6	12	5	2	10
4	8	12	6	4	24
4	9	15	8	1	8
5	9	15	9	3	27
5	9	15	10	2	20
11	1	11
12	2	24
15	3	45

--> ЧИТАТЬ ПОЛНОСТЬЮ <--