Реферат: Сетевое моделирование при планировании. Задача о коммивояжере...
х8 = 8
х9 = 19
Функционал в данной задаче равен –481, что не имеет смысла при заданных условиях. Однако, исходя из математической модели, функционал в данной задаче равен значению х9 . Таким образом, максимальная пропускная способность сети составит 19 тыс. тонн. При этом некоторые маршруты окажутся незадействованными (х4 и х6 ). График будет выглядеть следующим образом.
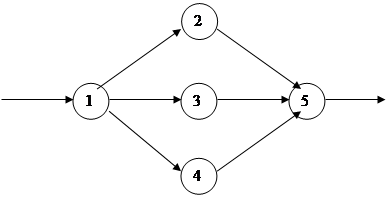
Задание №4
Тема: Системы массового обслуживания
Задача: Рационализация функционирования системы управления аэропортом на базе анализа марковских процессов
Различные аэропорты имеют отделы системы управления, функциональная связь которых и интенсивность потоков информации представлены на рисунке и в таблице 4.1.
Требуется вычислить вероятности состояний в стационарном режиме по значениям интенсивности перехода.
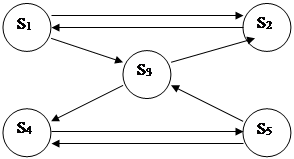
Таблица 4.1
Исходные данные
| Интенсивность потоков (переходов) | |||||||
| l12 | l13 | l21 | l32 | l34 | l45 | l53 | l54 |
| 3 | 2 | 1 | 3 | 2 | 2 | 3 | 1 |
Математическая модель
Примем за х1 , х2 , …, х5 предельные вероятности состояний в стационарном режиме пунктов S1 , S2 , …, S5 соответственно. Произведение вероятности состояния на интенсивность исходящих из этого пункта потоков равна произведению интенсивностей входящих потоков на вероятность состояния в стационарном режиме пунктов их отправления. Система уравнений Колмогорова для данной задачи в общем виде выглядит следующим образом:
(l13 + l12 )* х1 = l21 * х2 (1)
l21 * х2 = l12 * х1 + l32 * х3 (2)
(l32 + l34 )* х3 = l13 * х1 + l53 * х5 (3)
l45 * х4 = l34 * х3 + l54 * х5 (4)
(l54 + l53 )* х5 = l45 * х4 (5)
Кроме того, сумма всех вероятностей равна 1. При подстановке данных таблицы 4.1 и добавлении переменной х6 получаем:
5 х1 - х2 + х6 = 0 (1)
х2 - 3х1 - 3х3 + х6 = 0 (2)
5 х3 - 2х1 - 3х5 + х6 = 0 (3)
2 х4 - 2х3 – х3 + х6 = 0 (4)
4 х5 - 2х4 + х6 = 0 (5)
х1 + х2 + х3 + х4 + х5 + х6 = 1 (6)
![]() Функция цели: М х6 max
Функция цели: М х6 max
Таблица 4.2.
Исходная матрица
| № | х1 | х2 | х3 | х4 | х5 | х6 | Св.чл. | Знак |
| 1 | 5 | -1 | 0 | 0 | 0 | 1 | 0 | = |
| 2 | -3 | 1 | -3 | 0 | 0 | 1 | 0 | = |
| 3 | -2 | 0 | 5 | 0 | -3 | 1 | 0 | = |
| 4 | 0 | 0 | -2 | 2 | -1 | 1 | 0 | = |
| 5 | 0 | 0 | 0 | -2 | 4 | 1 | 0 | = |
| 6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = |
| Ф.ц. | 0 | 0 | 0 | 0 | 0 | М | max |
Решение
Функционал = -500
х1 = 0,125
х2 = 0,625
х3 = 0,083
х4 = 0,111
х5 = 0,055