Реферат: Системи масового обслуговування з очікуванням без обмеження на довжину черги

Враховуючи ті ж самі властивості стаціонарності і ординарності простіших (пуассонівських) потоків, одержимо:

,(11)

. (12)

Якщо підставити (11) і (12) у рівність (10), тоді матимемо:

.

Якщо відняти від обох частин останньої рівності , а далі розділити на , тоді запишемо

Тепер обчислимо границі від обох частин, якщо :

(13)

Таким чином отримуємо систему диференціальних рівнянь для обчислення – ймовірностей переходу від стану до стану СМО з чергою, що має скінченне число місць в накопичувачі:

(14)

Якщо спостерігати СМО достатньо довгий час , тоді розв’язок системи (14) можна знайти, якщо позначити (фінальні ймовірності) у вигляді:

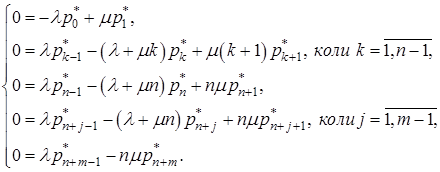(15)

Система (15) є лінійною, однорідною, алгебраїчною системою з невідомими . Для того, щоб знайти єдиний розв’язок системи (15) необхідно додати умову

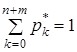.(16)

Раніше було доведено, що для усіх діє формула:

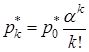, де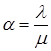

Тепер розглянемо -е рівняння системи (15) і обчислимо ,

.

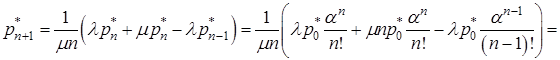
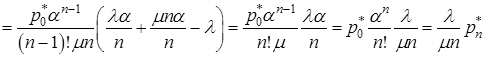Отже, одержали зв’язок і

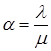де (17)

Нехай формула (17) є правильною для . Необхідно довести, що вона правильна і для . Для цього із системи (15) візьмемо рівняння з номером , отже

,

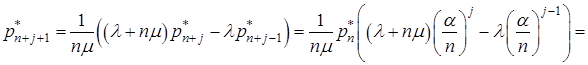
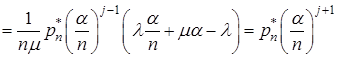тобто

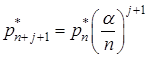.(18)

Тепер потрібно перевірити, що (18) правильна і для . Для цього необхідно взяти останнє рівняння системи (15), з нього маємо