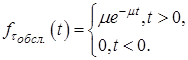Реферат: Системи масового обслуговування з очікуванням без обмеження на довжину черги

(37)

Випадкова величина не є дискретною, бо в точці і 1 функція розподілу має розрив. Якщо ввести функцію що має похідну , тоді можна записати щільність розподілу часу очікування обслуговування , тобто

(38)

,

де .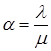

4. Середній час очікування початку обслуговування

Якщо врахувати (38) і формулу обчислення математичного сподівання випадкової величини, тоді можна обчислити середній час очікування початку обслуговування:

(39)

.

Відомо, що , тому другий інтеграл у (39) дорівнює нулю, тоді

.(40)

Оскільки для існування фінальних ймовірностей достатньо, щоб , тоді , звідки . Враховуючи це в (40), отримаємо:

.(41)

5. Середній час перебування заявки у СМО

Позначимо середній час перебування заявки в СМО через . Середній час перебування заявки в системі складається із часу очікування обслуговування і часу, що йде на обслуговування, тобто

,

тоді

.

Враховуючи (41) і те , що 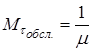, маємо

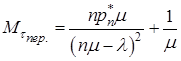. (42)

6. Функція розподілу випадкового часу перебування заявки у СМО

(43)

,

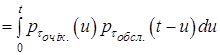де – щільність розподілу випадкового часу очікування обслуговування, що обчислюється за формулою (38), а – щільність розподілу випадкового часу обслуговування.