Реферат: Случайные процессы
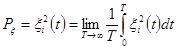
необходимо осуществить операции возведения в квадрат исследуемого процесса и интегрирования.
Для случайного процесса с ненулевым математическим ожиданием дисперсия (мощность переменной составляющей) равна
.
В соответствии с этим выражением при измерении полной мощности случайного процесса можно исключить постоянную составляющую и тем самым упростить измерение.
Для измерения ковариационной функции случайного процесса К(τ) необходимо осуществить операции задержки на различное время τ 
, умножения и интегрирования. Обычно ограничиваются измерением В(τ) в нескольких точках. При этом необходимо располагать набором перемножителей и линий задержки на фиксированное время задержки kΔt (чаще всего используют линию задержки с отводами).
Определение одномерной функции распределения вероятностей случайных процессов.
Для эргодических случайных процессов по одной реализации могут быть определены не только числовые характеристики, но и функция распределения вероятностей Р(τ) или плотность распределения вероятностей W(x). Функция распределения Р(х) определяется как относительное время пребывания одной реализацию длительностью Т (интервал наблюдения) ниже уровня x.
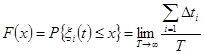
Соответственно плотность вероятности равна
,
где 
представляет собой относительное время пребывания реализации в интервале (х, х+Δх).
Таким образом, аппаратурное определение функции распределения эргодического процесса по одной реализации основано на измерении относительного времени пребывания случайного напряжения в интервале значений от U до (U + ΔU).
При реальных ΔU измеряется вероятность
,
для различных U и строится распределение вероятностей в виде гистограммы. Для получения функции плотности вероятностей W(U) необходимо аппроксимировать гистограмму непрерывной кривой или ожидаемым законом распределения, пользуясь критериями согласия.
Список использованной литературы:
1. Методическое указание к лабораторной работе «Вероятностные характеристики случайных сигналов».
2. «Теория передачи сигналов», А. Г. Зюко, «Радио и связь», 1986.