Реферат: Случайные величины в статистической радиотехнике

Законом распределения СВ называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину будем говорить, что она подчинена данному закону распределения.

Простейшей формой задания закона является табл. 1, в которой перечислены возможные значения СВ и соответствующие им вероятности.

Таблица 1

x1	x2	…	xN
p1	p2	…	pN

Однако такую таблицу невозможно построить для непрерывной СВ, поскольку для нее каждое отдельное значение не обладает отличной от нуля вероятностью.

Для количественной характеристики распределения используют зависимость вероятности события X < x , где x – некоторая текущая переменная, от x . Эта функция называется функцией распределения СВ X и обозначается F (x ): F (x ) = P (X < x ). Функцию распределения F (x ) иногда называют интегральной функцией распределения или интегральным законом распределения.

Функция распределения существует для всех СВ – как непрерывных, так и дискретных.

Сформулируем некоторые общие свойства F (x ):

1) F (x ) есть неубывающая функция своего аргумента, т.е. при x ₂ > x ₁ F (x ₂ ) > F (x ₁ );

2) на –¥F (x ) равна нулю, т.е. F (–¥) = 0;

3) F (¥) =

По определению, F (x ) при некотором x есть вероятность попадания СВ X в интервал от –¥ до x .

Для дискретной СВ распределение F (x ) имеет ступенчатый вид, причем величина каждого скачка равна вероятности значения, при котором имеется скачок F (x ).

При решении практических задач часто необходимо вычислять вероятность того, что СВ примет значение, заключенное в некоторых пределах, например от x ₁ доx ₂ . Это событие называется «попаданием СВ X на участок от x ₁ доx ₂ ». Выразим вероятность этого события через функцию распределения СВ X . Для этого рассмотрим два события:

– событие А , состоящее в том, что X < x ₂ ;

– событие В , состоящее в том, что X < x ₁ ;

– событие С , состоящее в том, что x ₁ < X < x ₂ .

Учитывая, что А = В + С , по теореме сложения вероятностей получим , или , откуда , т.е. вероятность попадания СВ на заданный участок равна приращению функции распределения на этом участке .

Пусть имеется непрерывная СВ X с функцией распределения F (x ), которую считаем непрерывной и дифференцируемой. Вычислим вероятность попадания этой СВ на участок от x до x + D x : , т.е. эта вероятность равна приращению функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка или среднюю вероятность, приходящуюся на единицу длины на этом участке. Кроме того, устремим Dx к нулю. В пределе получим производную от функции распределения:

.

Обозначим через f (x ). Полученная функция характеризует плотность , с которой распределяется значение СВ в данной точке x . Это и есть плотность вероятности . Иногда ее называют дифференциальным законом распределения СВ X .

Если X есть непрерывная СВ с плотностью вероятности f (x ), то величина f (x )dx есть элементарная вероятность, соответствующая событию – попаданию СВ X на отрезок dx . Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок dx и ограниченного сверху функцией f (x ).

Свойства плотности вероятности:

1) при всех x , поскольку вероятность не может быть отрицательной (кроме того, производная неубывающей функции не может быть отрицательной);

2) ;

3) ;

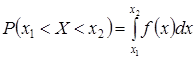4) свойство нормировки 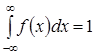, т.е. площадь, ограниченная графиком плотности вероятности и осью x , всегда равна 1 (кроме того, попадание СВ X в неограниченную с обеих сторон ось x является достоверным событием).

Во многих практических ситуациях нет необходимости характеризовать СВ плотностью вероятности. Часто бывает достаточно указать только отдельные числовые параметры, характеризующие в какой-то степени существенные черты распределения СВ, например, среднее значение, вокруг которого группируются возможные значения СВ; число, характеризующее степень разбросанности этих значений относительно среднего значения и т.д. Такие характеристики называются числовыми характеристиками СВ.

Математическое ожидание (МО) иногда называют средним значением СВ. Оно обозначается и для дискретной СВ определяется по формуле

.
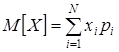