Реферат: Случайные величины в статистической радиотехнике

Математическим ожиданием СВ называют сумму произведений всех возможных значений СВ на вероятности этих значений.

Математическое ожидание СВ X связано со средним арифметическим значением наблюдаемых значений СВ при большом числе опытов так же, как и вероятность с частотой события, т.е. при увеличении числа опытов среднее арифметическое значение стремится к МО.

Для непрерывной СВ МО определяется по формуле

.

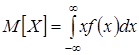Физически МО можно трактовать как координату центра тяжести тела (плотности вероятности). Единица измерения МО соответствует единице измерения СВ.

Моменты. Дисперсия. Среднеквадратическое отклонение. Начальным моментом s -го порядка для дискретной СВ X называется сумма вида 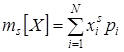. Для непрерывной СВ –

.

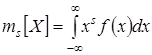Из этих формул видно, что МО есть не что иное, как первый начальный момент СВ X . Условно, используя знак МО, можно записать выражение для s -го начального момента, т.е. – начальным моментом s -го порядка СВ X называют МО s -й степени этой СВ.

Центрированной СВ , соответствующей СВ X , называют отклонение СВ X от ее МО, т.е. . Нетрудно убедиться, что МО центрированной СВ равно нулю. Моменты центрированной СВ называют центральными моментами . Таким образом, центральным моментом s -го порядка называют МО s - й степеницентрированной СВ : . Для непрерывной СВ s - й центральный момент выражают интегралом:

.

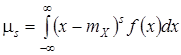Введем соотношения, связывающие центральные и начальные моменты различных порядков: ; ; ;…

Из всех моментов чаще всего в статистической радиотехнике применяют МО и вторые моменты – начальный и центральный. Второй центральный момент называют дисперсией СВ X . Для нее вводят специальное обозначение , или D_X .

Дисперсия характеризует степень разбросанности (или рассеивания) СВ X относительно математического ожидания и имеет размерность квадрата СВ X . На практике удобнее пользоваться величиной, размерность которой совпадает с размерностью СВ. Для этого из дисперсии извлекают квадратный корень. Полученную величину называют среднеквадратическим отклонением (СКО). Ее обозначают через . При извлечении квадратного корня из второго начального момента получается величина, названная среднеквадратическим значением (СКЗ). Часто используют формулу, связывающую основные моменты:

.

Третий центральный момент служит для характеристики асимметрии (или «скошенности») плотности вероятности. Если плотность вероятности симметрична относительно МО, то все моменты нечетного порядка равны нулю. Поэтому естественно в качестве характеристики асимметрии плотности вероятности выбрать какой-либо из нечетных моментов, из них простейший . Но чтобы иметь безразмерную величину, этот момент делят на куб среднеквадратического отклонения . Полученная величина носит название коэффициента асимметрии или просто асимметрии , обозначают ее через S_k :

.

Четвертый центральный момент служит для характеристики так называемой «крутости» (островершинности или плосковершинности) плотности вероятности. Эти свойства распределения описываются с помощью так называемого эксцесса: 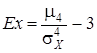. Число 3 вычитается из отношения потому, что для весьма распространенного в природе нормального закона это отношение равно трем.

Кроме рассмотренных моментов, используют иногда абсолютные моменты (начальные и центральные): ; . Из них чаще всего применяют первый абсолютный центральный момент , называемый средним арифметическим отклонением . Его используют наряду со среднеквадратическим отклонением для характеристики рассеивания СВ, для которых не существует дисперсии.

Кроме таких характеристик, используются понятия мода и медиана плотности вероятности. Модой (М) называют наиболее вероятное значение, соответствующее максимуму плотности вероятности (если таких максимумов несколько, то распределение называют полимодальным ). Медиана (Ме) – это такое значение СВ X , для которого P(X < Me) = P(X > Me). В случае симметричного одномодального (унимодального) распределения медиана совпадает с МО и модой.

Распределение Лапласа (двухсторонний экспоненциальный):

,

где m – МО; l – характеризует степень разбросанности X относительно m.

2. Биномиальное распределение (Бернулли):

.

Например, это распределение используется для определения вероятностей правильного обнаружения и ложной тревоги по пачке импульсов при заданных вероятностях обнаружения и вероятности ложной тревоги одного импульса в пачке.

3. Закон равномерной плотности вероятности.

Пример. Погрешность измерения напряжения с помощью вольтметра с дискретной шкалой (±(a – b)/2 – половина деления). МО есть (a + b)/2; дисперсия – (a – b)² /12; среднеквадратическое отклонение (a – b)/(2).

4. Нормальный (Гаусса) закон. Самый распространенный в природе:

.
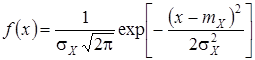