Реферат: Собственные вектора и собственные значения линейного оператора
Решение. Составим характеристическое уравнение:
|P – λ· E | =![]() = λ2 -5 λ+4=0
= λ2 -5 λ+4=0
Из квадратного уравнения найдем собственные значения линейного оператора λ1 =1, λ2 =4. Чтобы найти собственные векторы, решим матричные уравнения:
(P – λ1 E ) X =0 и (P – λ2 E ) X =0
В развернутом виде
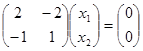 и
и 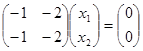
Соответствующие однородные системы:
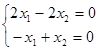
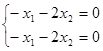
Общие решения систем:
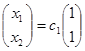 и
и 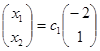 , где с1 , с2 є R
, где с1 , с2 є R
Таким образом, множество собственных векторов, отвечающих собственным значениям λ1 =1, λ2 =4, имеет вид ![]() ;
; ![]() , где с1 , с2 є R. Векторы a1 =(1, 1), a2 =(-2, 1), например, являются линейно независимыми. Они могут быть приняты в качестве нового базиса в пространстве R2 .
, где с1 , с2 є R. Векторы a1 =(1, 1), a2 =(-2, 1), например, являются линейно независимыми. Они могут быть приняты в качестве нового базиса в пространстве R2 .
Пусть e1 , e2 , …, en – собственные векторы линейного оператора ![]() в пространстве Rn , которые примем в качестве базиса. Тогда разложение векторов
в пространстве Rn , которые примем в качестве базиса. Тогда разложение векторов ![]() (e1 ),
(e1 ), ![]() (e2 ), …,
(e2 ), …, ![]() (en ) по базису e1 , e2 , …, en примет вид
(en ) по базису e1 , e2 , …, en примет вид
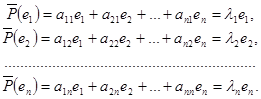
Отсюда следует, что aij = λ i , если i=j и aij =0, если i≠j. Поэтому в базисе, составленном из собственных векторов, матрица оператора будет иметь диагональный вид:
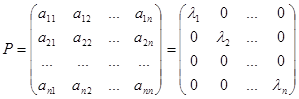
Симметричный оператор
Определение. Линейный оператор ![]() в евклидовом пространстве Rn называется симметричным, если для любых векторов x и y из пространства Rn выполняется равенство
в евклидовом пространстве Rn называется симметричным, если для любых векторов x и y из пространства Rn выполняется равенство
(![]() (x), y)= (x,
(x), y)= (x, ![]() (y))
(y))
Для того чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была симметрична.
Рассмотрим для простоты евклидово пространство R2 . Пусть в ортобазисе e1 , e2 заданы векторы x=(x1 , x2 ), y=(y1 , y2 ). Линейные операторы ![]() 1 и
1 и ![]() 2 определены своими матрицами:
2 определены своими матрицами:
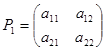 и
и 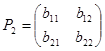 .
.
Вычислим векторы ![]() 1 (x) и
1 (x) и ![]() 2 (y):
2 (y):
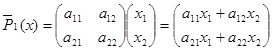 ,
,
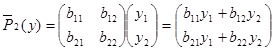 .
.
Найдем скалярные произведения (![]() (x), y) и (x,
(x), y) и (x, ![]() (y)):
(y)):
( ![]() (x), y)=(a11 x1 +a12 x2 ) y1 +(a21 x1 +a22 x2 ) y2 =a11 y1 x1 +a12 y1 x2 +a21 y2 x1 +a22 y2 x2 ,
(x), y)=(a11 x1 +a12 x2 ) y1 +(a21 x1 +a22 x2 ) y2 =a11 y1 x1 +a12 y1 x2 +a21 y2 x1 +a22 y2 x2 ,
(x, ![]() (y))= (b11 y1 +b12 y2 ) x1 +(b21 y1 +b22 y2 ) x2 =b11 x1 y1 +b12 x1 y2 +b21 x2 y1 +b22 x2 y2 .
(y))= (b11 y1 +b12 y2 ) x1 +(b21 y1 +b22 y2 ) x2 =b11 x1 y1 +b12 x1 y2 +b21 x2 y1 +b22 x2 y2 .
Найдем разность скалярных произведений:
(![]() ( x ), y ) – ( x ,
( x ), y ) – ( x , ![]() ( y )) = ( a 11 - b 11 ) x 1 y 1 +( a 21 - b 12 ) x 1 y 2 +( a 12 - b 21 ) x 2 y 1 +( a 22 - b 22 ) x 2 y 2 .
( y )) = ( a 11 - b 11 ) x 1 y 1 +( a 21 - b 12 ) x 1 y 2 +( a 12 - b 21 ) x 2 y 1 +( a 22 - b 22 ) x 2 y 2 .