Реферат: Сортировка данных в массиве

// Если индексы все еще в своих подсписках, то они указывают

// на два элемента, находящихся не в тех подсписках.

if(scanUp < scanDown)

{

// Поменять их местами

Swap(A[scanUp], A[scanDown]);

}

}

while(scanUp < scanDown);

// Скопировать элемент на который указывает точка разбиения

// в первый элемент первого подсписка, ...

A[low] = A[scanDown];

// а центральный элемент в точку разбиения

A[scanDown] = pivot;

// если первый подсписок (low...scanDown-1) имеет 2 или более

// элемента, выполнить для него рекурсивный вызов QuickSort

if(low < scanDown-1)

QuickSort(A, low, scanDown-1);

// если второй подсписок (scanDown+1...high) имеет 2 или более

// элемента, выполнить для него рекурсивный вызов QuickSort

if(scanDown+1 < high)

QuickSort(A, scanDown+1, high);

}

Вычислительная сложность «быстрой» сортировки

Общий анализ эффективности «быстрой» сортировки достаточно труден. Будет лучше показать ее вычислительную сложность, подсчитав число сравнений при некоторых идеальных допущениях. Допустим, что n – степень двойки, n = 2k (k = log2n), а центральный элемент располагается точно посередине каждого списка и разбивает его на два подсписка примерно одинаковой длины.

При первом сканировании производится n-1 сравнений. В результате создаются два подсписка размером n/2. На следующей фазе обработка каждого подсписка требует примерно n/2 сравнений. Общее число сравнений на этой фазе равно 2(n/2) = n. На следующей фазе обрабатываются четыре подсписка, что требует 4(n/4) сравнений, и т.д. В конце концов процесс разбиения прекращается после k проходов, когда получившиеся подсписки содержат по одному элементу. Общее число сравнений приблизительно равно

n + 2(n/2) + 4(n/4) + ... + n(n/n) = n + n + ... + n = n * k = n * log2n

Для списка общего вида вычислительная сложность «быстрой» сортировки равна O(n log2 n). Идеальный случай, который мы только что рассмотрели, фактически возникает тогда, когда массив уже отсортирован по возрастанию. Тогда центральный элемент попадает точно в середину каждого подсписка.

Если массив отсортирован по убыванию, то на первом проходе центральный элемент обнаруживается на середине списка и меняется местами с каждым элементом как в первом, так и во втором подсписке. Результирующий список почти отсортирован, алгоритм имеет сложность порядка O(n log2n).

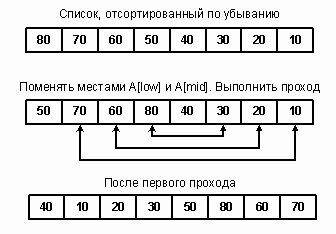
Рис.6