Реферат: Сортировка данных в массиве
На первом проходе производится n сравнений, а больший подсписок содержит n-1 элементов. На следующем проходе этот подсписок требует n-1 сравнений и дает подсписок из n-2 элементов и т.д. Общее число сравнений равно:
| n + n-1 + n-2 + ... + 2 = n(n+1)/2 - 1 |
Сложность худшего случая равна O(n2), т.е. не лучше, чем для сортировок вставками и выбором. Однако этот случай является патологическим и маловероятен на практике. В общем, средняя производительность «быстрой» сортировки выше, чем у всех рассмотренных нами сортировок.
Алгоритм QuickSort выбирается за основу в большинстве универсальных сортирующих утилит. Если вы не можете смириться с производительностью наихудшего случая, используйте пирамидальную сортировку – более устойчивый алгоритм, сложность которого равна O(n log2n) и зависит только от размера списка.
Сравнение алгоритмов сортировки массивов
Мы сравнили алгоритмы сортировки, испытав их на массивах, содержащих 4000, 8000, 10000, 15000 и 20000 целых чисел, соответственно. Время выполнения измерено в тиках (1/60 доля секунды). Среди всех алгоритмов порядка O(n2) время сортировки вставками отражает тот факт, что на i-ом проходе требуется лишь i/2 сравнений. Этот алгоритм явно превосходит все прочие сортировки порядка O(n2). Заметьте, что самую худшую общую производительность демонстрирует сортировка методом пузырька. Результаты испытаний показаны в таблице 1 и на рисунке 7.
Для иллюстрации эффективности алгоритмов сортировки в экстремальных случаях используются массивы из 20000 элементов, отсортированных по возрастанию и по убыванию. При сортировке методом пузырька и сортировке вставками выполняется только один проход массива, упорядоченного по возрастанию, в то время как сортировка посредством выбора зависит только от размера списка и производит 19999 проходов. Упорядоченность данных по убыванию является наихудшим случаем для пузырьковой, обменной и сортировки вставками, зато сортировка выбором выполняется, как обычно.
| n | Обменная сортировка | Сортировка выбором | Пузырьковая сортировка | Сортировка вставками |
| 4 000 | 12.23 | 17.30 | 15.78 | 5.67 |
| 8 000 | 49.95 | 29.43 | 64.03 | 23.15 |
| 10 000 | 77.47 | 46.02 | 99.10 | 35.43 |
| 15 000 | 173.97 | 103.00 | 223.28 | 80.23 |
| 20 000 | 313.33 | 185.05 | 399.47 | 143.67 |
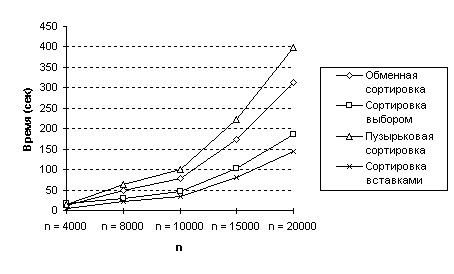
Рис.7 Сравнение сортировок порядка O(n2)
| n | Обменная сортировка | Сортировка выбором | Пузырьковая сортировка | Сортировка вставками |
| 8 000 (упорядочен по возрастанию) | 185.27 | 185.78 | 0.03 | 0.05 |
| 8 000 (упорядочен по убыванию) | 526.17 | 199.00 | 584.67 | 286.92 |
В общем случае QuickSort является самым быстрым алгоритмом. Благодаря своей эффективности, равной O(n log2n), он явно превосходит любой алгоритм порядка O(n2). Судя по результатам испытаний, приведенных в следующей таблице, он также быстрее любой из сортировок порядка O(n log2n), рассмотренных нами в прошлом номере. Обратите внимание, что эффективность «быстрой» сортировки составляет O(n log2n) даже в экстремальных случаях. Зато сортировка посредством поискового дерева становится в этих случаях O(n2) сложной, так как формируемое дерево является вырожденным.
| n | Турнирная сортировка | Сортировка посредством дерева | Пирамидальная сортировка | "Быстрая" сортировка |
| 4 000 | 0.28 | 0.32 | 0.13 | 0.07 |
| 8 000 | 0.63 | 0.68 | 0.28 | 0.17 |
| 10 000 | 0.90 | 0.92 | 0.35 | 0.22 |
| 15 000 | 1.30 | 1.40 | 0.58 | 0.33 |
| 20 000 | 1.95 | 1.88 | 0.77 | 0.47 |
| 8 000 (упорядочен по возрастанию) | 1.77 | 262.27 | 0.75 | 0.23 |
| 8 000 (упорядочен по убыванию) | 1.65 | 275.70 | 0.80 | 0.28 |
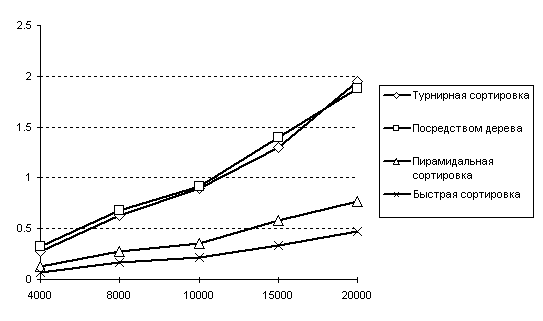
Рис.8 Сравнение сортировок порядка O(n log2n)
Сравнение сортировок
Эта программа осуществляет сравнение алгоритмов сортировки данных, представленных на рисунках 7 и 8. Здесь мы приводим только базовую структуру программы. Хронометраж производится с помощью функции TickCount, возвращающей число 1/60 долей секунды, прошедших с момента старта программы.
|
#include <iostream.h> #include "arrsort.h" // Перечислимый тип, описывающий начальное состояние массива данных. enum Ordering {randomorder, ascending, descending}; // Перечислимый тип, идентифицирующий алгоритм сортировки. enum SortType { SortTypeBegin, exchange = SortTypeBegin, selection, bubble, insertion, tournament, tree, heap, quick, К-во Просмотров: 680
Бесплатно скачать Реферат: Сортировка данных в массиве
|