Реферат: Состав и структура доходов и расходов населения

2) в зависимости от времени различают интервальные и моментные ряды.

3) в зависимости от расстояния между уровнями различают ряды с равноотстоящими и неравноотстоящими уровнями во времени.

Анализ скорости и интенсивности развития явления во времени осуществляется с помощью показателей, которые получаются в результате сравнения уровней между собой. К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста. При этом принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение – базисным.

Абсолютный прирост () характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста:

Если k=1, то уровень Yi-k является предыдущим для данного уровня, а абсолютные приросты изменения уровня будут цепными. Если же k постоянны для данного ряда, то абсолютные приросты будут базисными.

Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному, которое всегда представляет собой положительное число. Показатель интенсивности изменения уровня ряда – в зависимости от того, выражается он в коэффициентах или в процентах – принято называть коэффициентом роста или темпом роста . Эти формы по существу идентичны. Разница между ними только в единицах измерения. Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня (если коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы). В качестве базисного уровня в зависимости от цели исследования может приниматься какой-то постоянный для всех уровень (часто начальный уровень ряда), либо для каждого последующего предшествующий ему:

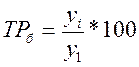или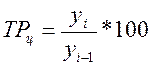

В первом случае говорят о базисных темпах роста, во втором – о цепных темпах роста.

Наряду с темпом роста можно рассчитать показатель темпа прироста , характеризующий относительную скорость изменения уровня ряда в единицу времени. Темп прироста показывает, на какую долю (или процент) уровень данного периода больше или меньше базисного. Темп прироста есть отношение абсолютного прироста к уровню ряда, принятого за базу:

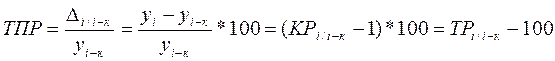
Если темп роста всегда положительное число, то темп прироста может быть положительным, отрицательным или равным нулю.

Средний уровень ряда динамики рассчитывается по средней хронологической. Методы расчета среднего уровня интервального и моментного рядов различны. Поскольку динамические ряды по среднедушевым доходам представляют собой равноотстоящие интервальные ряды, при расчете среднего уровня используется формула:

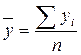
Обобщающим показателем скорости изменения явления во времени является средний абсолютный прирост:

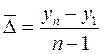
Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста, показывающий, во сколько раз в среднем за единицу времени изменился уровень динамического ряда. средний темп роста вычисляется по формуле средней геометрической из цепных коэффициентов роста:

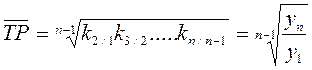
Средний темп прироста не может быть определен непосредственно по цепным или базисным показателям. Для его вычисления необходимо найти средний темп роста, а затем уменьшить его на единицу или на 100%:

Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития, присущей ряду. Методы анализа основной тенденции в рядах динамики разделяются на две основные группы:

1) сглаживание или механическое выравнивание

2) выравнивание с применением кривой, проведенной между уровнями таким образом, что бы она отображала тенденцию, присущую ряду и одновременно освободила его от незначительных колебаний.

Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени y=f(t). Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы, экспоненты и др.

Расчет параметров уравнений происходит по методу наименьших квадратов. Пример расчета параметров для полинома первой степени:

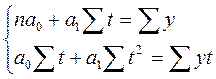
Параметры уравнения рассчитываются способом отсчета времени от условного нуля, то есть сумма времени становится равной 0. Тогда система упрощается и параметры равны:

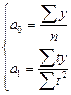
После проведения аналитического выравнивания обычно проводится прогнозирование значений уровня динамического ряда с использованием найденной формы полинома.